Perimeter of Circle Problems - page 12 of 14
Number of problems found: 280
- Determine 19953
The distance between the tip of the minute hand and the center of the dial is 12 mm. Determine the distance traveled by the tip in 45 min. (draw a clock face and a minute hand and realize the distance it will cover in 45 min.) - Circle described
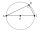The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle. - Hexagon in circle
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle. - Circle arc
The circle segment has a circumference of 135.26 dm and 2096.58 dm² area. Calculate the radius of the circle and the size of the central angle. - Outer contact of circles
Construct a circle k1 (S1; 1.5 cm), k2 (S2; 2 cm), and K3 (S3; 2.5 cm) so that they are always two outer contacts. Calculate the perimeter of the triangle S1S2S3. - Rectangle
In a rectangle with sides, 8 and 9 mark the diagonal. What is the probability that a randomly selected point within the rectangle is closer to the diagonal than any side of the rectangle? - Calculate 16223
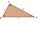The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Circular segment
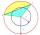Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - The amphitheater
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which spectators, P, Q, R, S, and T, see the stage at the greatest viewing angle? - Three
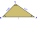Three points are given: A (-3, 1), B (2, -4), C (3, 3) a) Find the perimeter of triangle ABC. b) Decide what type of triangle the triangle ABC is. c) Find the length of the inscribed circle - Department 4220
Draw the line segment AB, AB = 5 cm. Draw a set of points 2 cm away from line AB. What is the district's department? - Larger perimeter
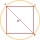A square and a circle pass through two adjacent vertices of the square (endpoints of side a) and the center of the opposite side (c). Which of the plane shape has a larger perimeter? - Circle from string
Martin has a long 628 mm string. He makes a circle from it. Calculate the radius of the circle. - A cylinder
A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm? - If we want
A children’s pool has the shape of a cylinder with a base diameter of 4 m and a depth of 50 cm (sketch, calculation, answer). a) Calculate the volume of water in liters that can be in the pool if it is filled to the brim. b) If we fill the pool only 75%, - What is bigger?
Which ball has a larger volume: a football with a circumference of 66 cm or a volleyball with a diameter of 20 cm? - Cone
The circular cone of height 14 cm and volume 4396 cm³ is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut. - Circumference 30781
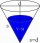How many square decimeters of decorative paper are needed to make cone-shaped carnival hats for 46 first-graders if the first-graders head circumference is 49 cm and the cap height is 33 cm? Is it necessary to add 3% paper to the folds? - Cylindrical 7804
The garden children's pool has the shape of a cylinder with a base diameter of 3.2 m and a depth of 60 cm. The water reaches 10 cm below the top edge. How many m² of the surface of the cylindrical wall of the pool is above the water? Rounds to the whole m - Winch drum
Originally an empty winch drum with a diameter of 20 cm and a width of 30 cm on the rescue car, he started winding a rope with a thickness of 1 cm from edge to edge. The winch stopped after 80 turns. It remains to spin 3.54m of rope (without hook). How lo
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
