Larger perimeter
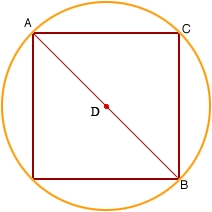
A square and a circle pass through two adjacent vertices of the square (endpoints of side a) and the center of the opposite side (c). Which of the plane shape has a larger perimeter?
Correct answer:
You need to know the following knowledge to solve this word math problem:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circle section
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Circumference 7143
Peter drew a regular hexagon, the vertices of which lay on a circle 16 cm long. Then, for each vertex of this hexagon, he drew a circle centered on that vertex that ran through its two adjacent vertices. The unit was created as in the picture. Find the ci - Circle and square
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Cylinders
The area of the side of two cylinders is the same rectangle of 48 cm × 38 cm. Which cylinder has a larger volume, and by how much?
- Intersection 81611
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides. - Perimeter 20283
If we increase the length of one pair of opposite sides of the square by 2 cm and the length of the other two sides by 1 cm, we will create a rectangle, the perimeter of which will be 10% larger than the perimeter of the original square. What is the side - Intersection of the lines
How many points do nine lines intersect in a plane, of which four are parallel, and of the other five, no two are parallel (and if we assume that only two lines pass through each intersection)?
