Circle and square
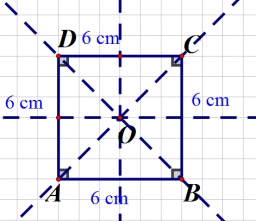
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and are looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- circle
- triangle
- square
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- MO circles
Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th - Quadrilateral 78874
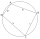Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Cylindrical 46021
Calculate the magnetic field energy of a cylindrical coil with 400 turns, a length of 0.4 m, and a radius of 20 mm. A current of 3A passes through the coil. (µo = 4π 10-7 H. M-1) - Calculate 70814
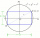The lengths of the sides AB and AD of the rectangle ABCD are in the ratio 3:4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
- Rectangle - parallelogram
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Equation 2604
The given triangle is ABC: A [-3; -1] B [5; 3] C [1; 5] Write the line equation that passes through the vertex C parallel to the side AB. - Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
