Calculate 70814
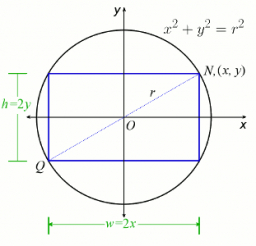
The length of the sides AB and AD of the rectangle ABCD are in the ratio 3:4. A circle k with a diameter of 10 cm describes a rectangle. Calculate the side lengths of a given rectangle.
Correct answer:
Tips for related online calculators
Check out our ratio calculator.
The Pythagorean theorem is the base for the right triangle calculator.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Quadrilateral 80729
Quadrilateral ABCD has side lengths AB=13cm, CD=3cm, AD=4cm. Angles ACB and ADC are right angles. Calculate the perimeter of quadrilateral ABCD. - Trapezoid RT
The plot has a shape of a rectangular trapezium ABCD, where ABIICD with a right angle at the vertex B. side AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. Lengths of the sides AB and CD are a ratio of 3:2. Calculate con - Circle and square
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Diagonal
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
- Quadrilateral 81097
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - Circumference 3088
In the parallelogram ABCD, the side AB is three times longer than the side BC. The circumference of the parallelogram is 20 cm. Find the lengths of the sides of the parallelogram. - Triangle in a square
In a square ABCD with side a = 6 cm, point E is the center of side AB, and point F is the center of side BC. Calculate the size of all angles of the triangle DEF and the lengths of its sides. - Rectangle - parallelogram
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Circumference 18443
In the parallelogram ABCD, the side AB is three times longer than the side BC. The circumference of the parallelogram is 20 cm. Determine the lengths of the sides of the parallelogram.
- Circumference 7052
The trapezoid ABCD is given (AB || CD, AB perpendicular to AD). Calculate its circumference if | AB | = 20cm, | CD | = 15cm, | AD | = 12cm. Pythagorean theorem - Right-angled 81019
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Circle and rectangle
The circle describes a rectangle with sides of 11.7 cm and 175 mm. What is its length? Calculate the area of the circle described by this circle. - Calculate 8252
Calculate in cm² the area of a circle whose diameter is equal to the length of the diagonal of a square ABCD with a side of 4cm. - Rhumbline
Find the circumference and area of the rhumbline ABCD if the short side AD has a length of 5 cm, and the heel of the height from D leading to the AB side divides the AB side into two sections of 3 cm and 4 cm.
- Trapezoidal prism
Calculate the surface of the quadrilateral prism ABCDA'B'C'D' with the trapezoidal base ABCD. The height of the prism is 12 cm; ABCD trapezoidal data: AB base length is 8 cm, CD base length is 3 cm, BC arm length is 4 cm, and AC diagonal length is 7 cm. L - Equilateral 4301
Triangle ABC is equilateral with a side length of 8 cm. Points D, E, and F are the sides AB, BC, and AC midpoints. Calculate the area of triangle DEF. In what ratio is the area of triangle ABC to the area of triangle DEF? - The sides
The sides of a rectangle are in a ratio of 2:3, and its perimeter is 1 1/4 inches. What are the lengths of its side? Draw it.
