Ratio + square (second power, quadratic) - practice problems
Number of problems found: 141
- A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - Two similar 2
 Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second?
Two similar polygons have corresponding sides 15 inches and 6 inches. If the area of the first is 2700 square inches, what is the area of the second? - A group
 A group of young men decides to raise ksh 480,000 to start a business. Before the actual payment was made, four members pulled out, and each of the remaining had to pay an additional ksh 20,000. Determine the original number of members.
A group of young men decides to raise ksh 480,000 to start a business. Before the actual payment was made, four members pulled out, and each of the remaining had to pay an additional ksh 20,000. Determine the original number of members. - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
- Dimensions 83092
 On the 1:75 scale plan, the building plot is a rectangle with 60 cm and 50 cm dimensions. If 1 m² of land costs 80 euros, what is the price of the land?
On the 1:75 scale plan, the building plot is a rectangle with 60 cm and 50 cm dimensions. If 1 m² of land costs 80 euros, what is the price of the land? - Centimeters 82996
 The volume of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Determine the height of the trapezoid in centimeters.
The volume of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Determine the height of the trapezoid in centimeters. - Coordinate 82855
 What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system?
What is the ratio of the distance of the nearest and farthest point of the circle described by the equation x2+y2-16x-12y+75=0 from the origin of the coordinate system? - Calculate 81939
 The block surface is 5,632 m². The lengths of the edges are in the ratio 1: 2 : 3. Calculate the volume of the cuboid.
The block surface is 5,632 m². The lengths of the edges are in the ratio 1: 2 : 3. Calculate the volume of the cuboid. - Square-shaped 81445
 The area of the square-shaped room on the drawing with a scale of 1:150 is 6 cm square. Determine the actual area of the room in square meters.
The area of the square-shaped room on the drawing with a scale of 1:150 is 6 cm square. Determine the actual area of the room in square meters.
- Perimeters 81399
 Two squares are given. The first has a side length of 5 cm, the second 10 cm. Write the ratio of: for a- of their sides for b- their perimeters for c- their areas
Two squares are given. The first has a side length of 5 cm, the second 10 cm. Write the ratio of: for a- of their sides for b- their perimeters for c- their areas - Quadrilateral 81385
 A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created.
A regular quadrilateral pyramid with base edge length a = 15cm and height v = 21cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created. - Determine 81311
 The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm.
The surface of the rotating cone and its base area is in the ratio 18:5. Determine the volume of the cone if its body height is 12 cm. - Square 81238
 A forest with a square plan has an area of 4 square km. What side will the square have on a 1:50,000 scale map?
A forest with a square plan has an area of 4 square km. What side will the square have on a 1:50,000 scale map? - Right-angled 81126
 In a right-angled triangle, the hypotenuse has a length of 24 cm. The heel of the height on the hypotenuse divides it into two parts in a ratio of 2:4. What size in cm is the height at the hypotenuse? Calculate the perimeter of this right triangle in cent
In a right-angled triangle, the hypotenuse has a length of 24 cm. The heel of the height on the hypotenuse divides it into two parts in a ratio of 2:4. What size in cm is the height at the hypotenuse? Calculate the perimeter of this right triangle in cent
- Circumscribed 81025
 A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere.
A cube with a volume of 4096 cm³ is described and inscribed by a sphere. Calculate how many times the volume of the circumscribed sphere is greater than the inscribed sphere. - Right-angled 81019
 In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC.
In the right-angled triangle ABC (AB is the hypotenuse), a : b = 24 : 7, and the height to the side c = 12.6 cm applies. Calculate the lengths of the sides of triangle ABC. - Smaller 81015
 Divide the content of the garden in the shape of a square S=153m² in a ratio of 2:7. What part of the garden does the smaller part occupy?
Divide the content of the garden in the shape of a square S=153m² in a ratio of 2:7. What part of the garden does the smaller part occupy? - Centimeters 80859
 Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm².
Triangle ABC and triangle ADE are similar. Calculate in square centimeters the area of triangle ABC if the length of side DE is 12 cm, the length of side BC is 16 cm, and the area of triangle ADE is 27 cm². - Equilateral 80851
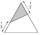 Kornelia cut off the colored part from the equilateral triangle. The shortest side of the colored triangle is 1/3 the length of the side of the original triangle. Calculate what part of the triangle she cut off.
Kornelia cut off the colored part from the equilateral triangle. The shortest side of the colored triangle is 1/3 the length of the side of the original triangle. Calculate what part of the triangle she cut off.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
