Reason - math word problems - page 66 of 108
Number of problems found: 2157
- Z9–I–4 MO 2017
Numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 were prepared for a train journey with three wagons. They wanted to sit out so that three numbers were seated in each carriage, and the largest of the three was equal to the sum of the remaining two. The conductor sai - Word MATEMATIKA
How many words can be created from the phrase MATEMATIKA by changing the letters' order, regardless of whether the words are meaningful? - Big number
What is the remainder when dividing 10 by 9 to 47 - 111? - Remainder
A is an arbitrary integer that gives remainder 1 in the division with 6. B is a random integer that provides the remainder with division by two. What makes remainder in a division by three products of numbers A x B? - Candies - coloured
There were red and green candies in the tin. Čenek ate 2/5 of all the red candies, and Zuzka ate 3/5 of all the green candies. Now, the red candies make up 3/8 of all the candies in the can. How many candies were originally in the can? - Difference 5419 Peter said to Paul: "Write a two-digit natural number with the property that if you subtract from it a two-digit natural number written in reverse, you get the difference 63. Which number could Paul have written?" Specify all options.
- Repeating digits There is a thousand one-digit number, which consists of repeating digits 123412341234. What remainder gives this number when dividing by nine?
- Intersection of the altitudes
In the acute triangle KLM, the angle KLM is 68°. Point V is the intersection of the altitudes, and P is the foot of the altitude on the side LM. The angle P V M axis is parallel to the side KM. Compare the sizes of angles MKL and LMK. - Double-digit 5411
Anička and Blanka each wrote one double-digit number, which started with a seven. The girls chose different numbers. Then, each inserted a zero between the two digits, giving them a three-digit number. Everyone subtracted their original two-digit number f - MO Z6-I-2 2017
Erika wanted to offer chocolate to her three friends. When she took it out of her backpack, she found that it was broken, as shown in the picture. (The marked squares are identical.) The girls have agreed not to break the chocolate anymore and will draw l - Asymmetric 5407
Find the smallest natural number k for which the number 11 on k is asymmetric. (e.g. 11² = 121) - Sweethearts 5403
Four sweethearts eat ten cakes in 30 minutes. How many minutes will 27 cakes last for nine sweets? - Adela number Adela had two numbers written on the paper. When she added their greatest common divisor and least common multiple, she was given four different numbers less than 100. She was amazed that if she divided the largest of these four numbers by the least, she
- One hundred stamps
A hundred letter stamps cost a hundred crowns. Its costs are four levels - twenty-tenths, one crown, two-crown, and five-crown. How many are each type of stamp? How many does the problem have solutions? - Average age
The average age of all people at the celebration was equal to the number of people present. After the departure of one person who was 29 years old, the average age was again equal to the number present. How many people were original to celebrate? - Warmer weather
This morning it was -6 °C. What temperature did the thermometer show yesterday if it was three times warmer? - Something 5385
Janko got pocket money and wants to buy something good for it. If he purchased four cakes, it would increase by 0.50 euros. If he wanted to buy five cakes, he would miss 0.60 euros. He would spend all his pockets on the rest if he bought two cakes and thr - Identity
123456789 = 100 Correct the given identity/equation only using three plus or minus signs. - MO8-Z8-I-5 2017
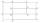Identical rectangles ABCD and EFGH are positioned such that their sides are parallel to the same. The points I, J, K, L, M, and N are the intersections of the extended sides, as shown. The area of the BNHM rectangle is 12 cm2, the rectangle MBC - Reading book
Susan read a 250-page book. On the first day, she read 20% of the book. On the second day, half of the remaining pages. How many pages of the book has it unread?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
