Right triangle practice problems - page 29 of 86
Number of problems found: 1716
- Perpendiculars 66274
The perpendiculars of a right triangle have 30 cm and 40 cm lengths. What is the height of the triangle? - Distance 64804
Dan is the square ABCD. At its diagonal AC lies point E. The distance AB is equal to the distance AE. What is the size of the EBC angle? - Legs and ratio
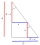For the legs of a right triangle, a : b = 6:8. The hypotenuse has a length of 61 cm. Calculate the perimeter and area of this triangle. - RT a-b-x
There is a right triangle with legs long a, b, and hypotenuse long x. Given that a = 6 cm and b = 9 cm, work out x. Give your answer as an exact surd. - An equilateral
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle? - Equilateral triangle
A square is inscribed into an equilateral triangle with a side of 10 cm. Calculate the length of the square side. - The pole
A 4 m bullet supports the telegraph pole. It is at 3/4 of pole height, and the end is at a distance of 2.5 m from the pole post. Calculate the height of the telegraph pole. - Cableway
The cableway has a length of 1800 m. The horizontal distance between the upper and lower cable car station is 1600 m. Calculate how much meters altitude is higher upper station than at the base station. - Triangle 63244
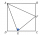The area of the ABCD square in the picture is 36 cm². Points E and F are the centers of the square BC and CD sides. What is the area of the triangle AEF in cm²? - Calculate 27441
Calculate the length of the side of the square if the size of the diagonal u = 9.9 cm is entered. - Height
Calculate the height of the equilateral triangle if its perimeter is 31. - Base and longest side
The base of a right-angled triangle is 10 centimeters, and the longest side is 26 centimeters. What is the area of the triangle? - The right triangle
The right triangle ABC has a leg a = 36 cm and an area S = 540 cm². Calculate the length of the leg b and the median t2 to side b. - Alpha angle
Right triangle. Given: side c = 15.8 and angle alpha = 73°10'. Calculate side a, b, angle beta, and an area. - Ladder
10 meters long ladder is leaning against the wall of the well, and its lower end is 1 meters from this wall. How high from the bottom of a well is the top edge of the ladder? - Isosceles right triangle
Calculate the area of an isosceles right triangle whose perimeter is 810 cm. - Vertices of RT
Show that the points P1 (5,0), P2 (2,1) & P3 (4,7) are the vertices of a right triangle. - Against 82851
A 3.4 m long ladder is leaning against a wall. Its lower end is 1.6 m away from the wall. At what height does the ladder touch the wall? - Determine 82595 A ladder is 7 meters long and is leaning against a wall so that its lower end is 4 meters away from the wall. Determine how high the ladder reaches
- Arithmetic 80808
The lengths of the sides of a right triangle form the first 3 terms of the arithmetic sequence. Its area is 6 cm². Find length of its sides.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
