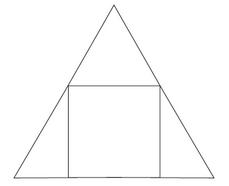
Equilateral triangle
A square is inscribed into an equilateral triangle with a side of 10 cm. Calculate the length of the square side.
Final Answer:
Tips for related online calculators
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Calculation of an equilateral triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraplanimetricsbasic operations and conceptsgoniometry and trigonometryGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Circle perimeters
An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle? - Calculate
Calculate the length of a side of the equilateral triangle with an area of 50cm². - Rhombus
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus. - Triangle side
I have a circle with a diameter of 6.4 cm. I need to find out the length of the side of an equilateral triangle inscribed in a circle. - Similarity coefficient
The similarity ratio of two equilateral triangles is 4.3 (i.e., 43:10). The length of the side of the smaller triangle is 7.5 cm. Calculate the perimeter and area of the larger triangle. - Circle section
An equilateral triangle with side 33 is an inscribed circle section whose center is in one of the triangle's vertices, and the arc touches the opposite side. Calculate: a) the length of the arc b) the ratio between the circumference to the circle sector a - Square circles
Calculate the length of the described and inscribed circle to the square ABCD with a side of 5cm.
