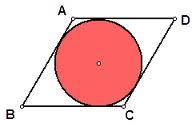
Rhombus

It is given a rhombus of side length a = 19 cm. Touchpoints of inscribed circle divided his sides into sections a₁ = 5 cm and a₂ = 14 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.

Correct answer:

r =  8.4 cm
u₁ =  19.5 cm
u₂ =  32.6 cm

Step-by-step explanation:

$$\begin{gathered} a_1=5\text{ cm } \\ {a}_2=14\text{ cm } \\ a=a_1+a_2=5+14=19\text{ cm } \\ {r}^2=a_1\cdot a_2 \\ r=\sqrt{a_1\cdot a_2}=\sqrt{5\cdot 14}=\sqrt{70}=8.4\text{ cm} \end{gathered}$$

$$\begin{gathered} (u_1\mathrm{/}2{)}^2=r^2+a_1^2 \\ {u}_1=2\cdot \sqrt{r^2+a_1^2}=2\cdot \sqrt{8.3666^2+5^2}=2\sqrt{95}=19.5\text{ cm} \end{gathered}$$

$$\begin{gathered} (u_2\mathrm{/}2{)}^2=r^2+a_2^2 \\ {u}_2=2\cdot \sqrt{r^2+a_2^2}=2\cdot \sqrt{8.3666^2+14^2}=2\sqrt{266}=32.6\text{ cm} \end{gathered}$$

Try another example

Related math problems and questions:

• Rhombus and inscribed circle
  It is given a rhombus with side a = 6 cm and the radius of the inscribed circle r = 2 cm. Calculate the length of its two diagonals.
• Circle in rhombus
  In the rhombus is an inscribed circle. Contact points of touch divide the sides to parts of length 19 cm and 6 cm. Calculate the circle area.
• Diagonals of the rhombus
  Calculate height of rhombus whose diagonals are 12 cm and 19 cm.
• Diagonals in diamons/rhombus
  Rhombus ABCD has side length AB = 4 cm and a length of one diagonal of 6.4 cm. Calculate the length of the other diagonal.
• Diagonals
  A diagonal of a rhombus is 20 cm long. If it's one side is 26 cm, find the length of the other diagonal.
• Rhombus and diagonals
  The lengths of the diamond diagonals are e = 48cm, f = 20cm. Calculate the length of its sides.
• Rhombus IV
  Calculate the length of the diagonals of the rhombus, whose lengths are in the ratio 1: 2 and a rhombus side is 35 cm.
• Rhombus diagonals
  In the rhombus ABCD are given the sizes of diagonals e = 24 cm; f = 10 cm. Calculate the side length of the diamond and the size of the angles, calculate the content of the diamond
• Diagonals
  Given a rhombus ABCD with a diagonalsl length of 8 cm and 12 cm. Calculate the side length and content of the rhombus.
• Diamond side
  The diagonals of the diamond are 18 cm and 14 cm long. Calculate the length of the diamond side.
• Rhombus
  The rhombus has diagonal lengths of 4.2cm and 3.4cm. Calculate the length of the sides of the rhombus and its height
• Diamond
  The side length of the diamond is 35 cm, and the length of the diagonal is 56 cm. Calculate the height and length of the second diagonal.
• Rhombus and diagonals
  The rhombus area is 150 cm², and the ratio of the diagonals is 3:4. Calculate the length of its height.
• Construct rhombus
  Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm
• Ratio of sides
  Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in ratio 2 to 7.
• RT - inscribed circle
  In a rectangular triangle has sides lengths> a = 30cm, b = 12.5cm. The right angle is at the vertex C. Calculate the radius of the inscribed circle.
• The diamond
  The diamond has sides of 35 cm and the diagonals are in a ratio of 1: 2. Calculate the lengths of the diagonals.