Rounding - math word problems - page 23 of 28
Number of problems found: 541
- Rhombus 2
Calculate the rhombus area with a height v=48 mm and shorter diagonal u = 60 mm long. - Jumps
At least how many jumps must a frog do to overcome the distance of 7 meters? The jump of a frog is 18 cm long. - Clock hands
The hands-on clock shows the time as 12 hours and 2 minutes. Three hours later, calculate the size of an acute angle between the clock hands. - Tent
A pyramid-shaped tent has a base square with a side length of 2 m and a height of 1.7 m. How many meters of canvas is needed to make it if we should add 10% for waste? - Bottles of juice
How many 2-liter bottles of juice need to buy if you want to transfer the juice to 50 pitchers' rotary cone shape with a diameter of 24 cm and a base side length of 1.5 dm? - Spherical cap
What is the surface area of a spherical cap, the base diameter 27 m, and height 2 m? - Goat and circles
What is the radius of a circle centered on the other circle, and is the intersection of the two circles equal to half the area of the first circle? This task is the mathematical expression of the role of agriculture. The farmer has circular land on which - Cathethus and the inscribed circle
A right triangle is given one cathetus long 14 cm and the radius of the inscribed circle of 5 cm. Calculate the area of this right triangle. - Sphere - parts
Calculate the area of a spherical cap, which is part of an area with a base radius ρ = 8 cm and a height v = 4.2 cm. - Pit
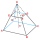The pit is 1.2 m deep and in the shape of a truncated pyramid with a rectangular base. Its length and width are the top 3 × 1.5 m and the bottom 1 m × 0.5 m. To paint one square meter of the pit, we use 0.8 l of green paint. How many liters of paint are n - Cross-sections of a cone
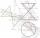Cone with base radius 15 cm and height 20 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Snowman 2
On the medal, which has the shape of a circle with a diameter 18 cm, is sketched a snowman so that the following requirements are met: 1. snowman is composed of three circles, 2. space over the snowman is the same as under it, 3. diameters of all circles - Two workers
Two workers will do certain work for 12 days. After eight days of working, one was removed, and the other finished the job alone in 10 days. For how many days would you do this work alone for each worker? - Snowman
In a circle with a diameter of 40 cm are drawn three circles (as a snowman) where: its diameters are integers, each larger circle diameter is 2 cm larger than the diameter of the previous circle. Determine the snowman height if we wish for the highest sno - Christmas
Exactly after 114 hours, we sit down at the Christmas Eve table. What day and what time was it when Dad said this sentence? They sit at the Christmas Eve table exactly at the 18-o'clock (6 PM). - Rounding
The following numbers round to the thousandth: - Tiles
From how many tiles, 20 cm by 30 cm, we can build a square of maximum dimensions if we have a maximum of 275 tiles. - Box
The cardboard is a box-shaped quadrangular prism with a rhombic base. Rhombus has a side 5 cm, one diagonal 8 cm long, and the box's height is 12 cm. The package will open at the top. How many cm² of cardboard do we need to cover overlap and joints that a - To thousands
Round to thousands of following numbers: 75225492791426955863585754416 - Remainders
It is given a set of numbers { 200; 261; 331; 345; 487; 554 }. Divide these numbers by number 80 and determine a set of remainders. As a result, write the sum of these remainders.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
