Flowerbed
The flowerbed has the shape of a truncated pyramid. The bottom edge of the base a = 10 m, and the upper base b = 9 m. The deviation angle between the edge and the base is alpha = 45°. What volume is needed to make this flowerbed? How many plants can be planted if one m2 = 100 plants?
Final Answer:

Tips for related online calculators
Do you know the volume and unit volume, and want to convert volume units?
Do you want to round the number?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to round the number?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
arithmeticsolid geometryplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Pyramid planting
 The flower bed has the shape of a regular 4-sided pyramid. The edge of the lower plinth is 10 m, and the upper plinth is 9 m. The deviation of the side wall from the base is 45 degrees. How many plantings should be purchased if 90 are needed to plant 1 sq
The flower bed has the shape of a regular 4-sided pyramid. The edge of the lower plinth is 10 m, and the upper plinth is 9 m. The deviation of the side wall from the base is 45 degrees. How many plantings should be purchased if 90 are needed to plant 1 sq - Regular quadrangular pyramid
 How many square meters are needed to cover the shape of a regular quadrangular pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%.
How many square meters are needed to cover the shape of a regular quadrangular pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%. - Truncated pyramid
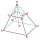 The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - Wooden bowls
 Twenty wooden bowls in the shape of a truncated cone should be painted on the outside and inside with wood varnish. We need 0.1 l of paint to paint 200 cm². How many liters of paint do we have to buy if the bowls are 25 cm high, the bottom of the bowl has
Twenty wooden bowls in the shape of a truncated cone should be painted on the outside and inside with wood varnish. We need 0.1 l of paint to paint 200 cm². How many liters of paint do we have to buy if the bowls are 25 cm high, the bottom of the bowl has - Digging a pit
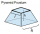 The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit.
The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit. - In a regular 5
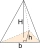 In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane.
In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane. - Truncated pyramid
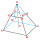 Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees.
Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees.
