Cathethus and the inscribed circle
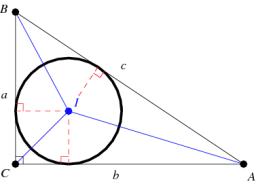
A right triangle is given one cathetus long 14 cm and the radius of the inscribed circle of 5 cm. Calculate the area of this right triangle.
Correct answer:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
See also our right triangle calculator.
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
See also our right triangle calculator.
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- rounding
- planimetrics
- right triangle
- circle
- area of a shape
- triangle
- basic functions
- percentages
- numbers
- fractions
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- OK circle
The right triangle has hypotenuse long 33 and one cathetus long 17. Calculate the radius (circumradius) of the circle described. - Circumscribed 83152
Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle. - Subtended 83194
A circle k with a center at point S and a radius of 6 cm is given. Calculate the size of the central angle subtended by a chord 10 cm long. - Construct rhombus
Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm
- Rhombus and inscribed circle
It is given a rhombus with side a = 6 cm and the inscribed circle r = 2 cm radius. Calculate the length of its two diagonals. - Quadrilateral 78874
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Rhombus
It is given a rhombus with a side length of a = 20 cm. Touchpoints of the inscribed circle divided its sides into sections a1 = 13 cm and a2 = 7 cm. Calculate the radius r of the circle and the length of the diagonals of the rhombus.
