Sine + The Law of Sines - practice problems
Number of problems found: 35
- Inaccessible 82710
 Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you.
Determine the distance between two inaccessible places K, L, if the angles KAL=62°10", LAB=41°23", KBL=66°34", and LBA were measured from points A, B, which are 870 m apart = 34°52". Thank you. - Observatories A,B
 The target C is observed from two artillery observatories, A and B, 296 m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target C from observatory A.
The target C is observed from two artillery observatories, A and B, 296 m apart. At the same time, angle BAC = 52°42" and angle ABC = 44°56". Calculate the distance of the target C from observatory A. - Perpendicular forces
 Distribute the force of magnitude F = 100 N into two perpendicular components with magnitudes F1 and F2 so that the angle between forces F1 and F is 43°52'.
Distribute the force of magnitude F = 100 N into two perpendicular components with magnitudes F1 and F2 so that the angle between forces F1 and F is 43°52'. - The cosine law
 Solve the unknown dimensions for the following triangle: Triangle ABC: Angle A=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of
Solve the unknown dimensions for the following triangle: Triangle ABC: Angle A=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of - A ship
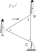 A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57°
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Triangle 75
 Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1.
Triangle ABC has angle C bisected and intersected AB at D. Angle A measures 20 degrees, and angle B measures 40 degrees. The question is to determine AB-AC if length AD=1. - Observatory and aircraft
 The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee
The aircraft flying towards the observatory was aimed at a distance of 5300 m at an elevation angle of 28º and after 9 seconds at a distance of 2400 m at an elevation angle of 50º. Calculate the distance the plane has flown in this time interval, its spee
- An azimuth
 The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started.
The patrol had started at a designated marching angle (an azimuth) of 13°. After 9 km, the azimuth's angle changed to 62°. The patrol went 10 km in this direction. Find the distance from where the patrol started. - Inaccessible direct
 Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B, - Determine 67754
 Adam (A) stands on one river bank, and Bedrich (B) stands on the other. To determine their distance, the base AC with a length of 136 m and the angles CAB with a size of 70°21' and ACB with a size of 43°44' were measured on one river bank. What is the dis
Adam (A) stands on one river bank, and Bedrich (B) stands on the other. To determine their distance, the base AC with a length of 136 m and the angles CAB with a size of 70°21' and ACB with a size of 43°44' were measured on one river bank. What is the dis - Magnitudes 64704
 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Hypotenuse and center
 Point S is the center of the hypotenuse AB of the right triangle ABC. Calculate the area of triangle ABC if the line on the hypotenuse is 0.2 dm long and if angle ∢ACS is 30°.
Point S is the center of the hypotenuse AB of the right triangle ABC. Calculate the area of triangle ABC if the line on the hypotenuse is 0.2 dm long and if angle ∢ACS is 30°. - Two artillery
 Objective C we observe from two artillery observatories, A and B, which are 975 m apart. The size of the BAC angle is 63°, and the size of ABC is 48°. Calculate the distance of points A and C.
Objective C we observe from two artillery observatories, A and B, which are 975 m apart. The size of the BAC angle is 63°, and the size of ABC is 48°. Calculate the distance of points A and C. - Cosine
 Cosine and sine theorem: Calculate all unknown values (side lengths or angles) from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm
Cosine and sine theorem: Calculate all unknown values (side lengths or angles) from triangle ABC. c = 2.9 cm; β = 28°; γ = 14° α =? °; a =? cm; b =? cm - Cosine
 Cosine and sine theorem: Calculate all unknown values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Cosine and sine theorem: Calculate all unknown values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
- Calculate triangle
 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and areas if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and areas if given a=40cm, b=57cm, and c=59cm. - Triangle's centroid
 In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t
In the triangle ABC the given lengths of its medians tc = 9, ta = 6. Let T be the intersection of the medians (triangle's centroid), and the point S is the center of the side BC. The magnitude of the CTS angle is 60°. Calculate the length of the BC side t - Triangle - sines
 The sum of the lengths of the two sides b + c = 12 cm Beta angle = 68 Gamma angle = 42 draw triangle ABC
The sum of the lengths of the two sides b + c = 12 cm Beta angle = 68 Gamma angle = 42 draw triangle ABC - Viewing angle
 The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure?
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - Sine theorem 2
 From the sine theorem, find the ratio of the sides of a triangle whose angles are 30°, 60°, and 90°.
From the sine theorem, find the ratio of the sides of a triangle whose angles are 30°, 60°, and 90°.
Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation. Sine - practice problems. The Law of Sines - practice problems.
