Calculate triangle
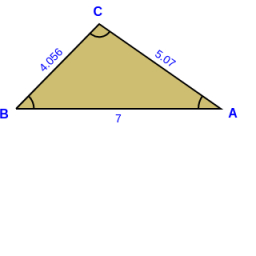
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Triangle
Calculate the heights of the triangle ABC if the sides of the triangle are a=82, b=44, and c=53. - Triangles
Find out whether the given sizes of the angles can be interior angles of a triangle: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3' - Similarity coefficient
The triangles ABC and A'B'C' are similar to the similarity coefficient 2. The sizes of the angles of the triangle ABC are α = 35° and β = 48°. Find the magnitudes of all angles of triangle A'B'C'. - Area and two angles
Calculate the size of all sides and internal angles of a triangle ABC if it is given by area S = 501.9; and two internal angles α = 15°28' and β = 45°. - Determine 5324
An isosceles triangle with base c and arms a is given by: a = 50.3 cm c = 48.2 cm Determine the interior angles and heights of the base c. - Triangle 7142
ABC triangle, alpha = 54 degrees 32 minutes, beta = 79 degrees. What are the sizes of the exterior angles? - Rhombus diagonals
In the rhombus ABCD are given the sizes of diagonals e = 24 cm; f = 10 cm. Calculate the side length of the diamond and the size of the angles, calculate the area of the diamond. - Triangle 2668
The triangle ABC has side lengths a = 14 cm, b = 20 cm, c = 7.5 cm. Find the sizes of the angles and the area of this triangle. - Triangle SSS
Calculate the perimeter and area of a triangle ABC if a=53, b=46, and c=40. - Construct 25851
A. Construct ∆ABC such that c = 55 mm, α = 45 °, β = 60 °. B. Draw any acute triangle and construct its heights. - Angles by cosine law
Calculate the size of the angles of the triangle ABC if it is given by: a = 3 cm; b = 5 cm; c = 7 cm (use the sine and cosine theorem). - Sss triangle
Calculate the area and heights in the triangle ABC by sides a = 8cm, b = 11cm, c = 12cm - Gamma angle
Find the magnitude of the gamma angle in triangle ABC if: α = 38° 56' and β = 47° 54'. - Equilateral 2543
a) The perimeter of the equilateral triangle ABC is 63 cm. Calculate the side sizes of the triangle and its height. b) A right isosceles triangle has an area of 40.5 square meters. How big is his circuit? c) Calculate the square's area if the diagonal's s - Right triangle
Calculate the length of the remaining two sides and the angles in the rectangular triangle ABC if a = 10 cm, angle alpha = 18°40'. - Calculate 3526
Calculate the height size in the triangle ABC if the side length a = 20cm and the area of the triangle is 50 cm square. - Right triangle trigonometrics
Calculate the size of the remaining sides and angles of a right triangle ABC if it is given: b = 10 cm; c = 20 cm; angle alpha = 60°, and the angle beta = 30° (use the Pythagorean theorem and functions sine, cosine, tangent, cotangent)
