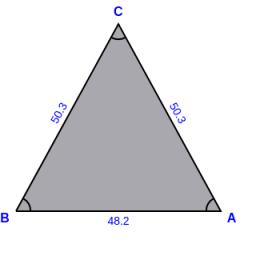
Isosceles triangle
An isosceles triangle with base c and arms a is given by: a = 50.3 cm c = 48.2 cm
Determine the interior angles and heights of the base c.
Determine the interior angles and heights of the base c.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Calculation of an isosceles triangle.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Calculation of an isosceles triangle.
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Isosceles triangle
 Calculate the size of the interior angles and the length of the base of the isosceles triangle if the arm's length is 17 cm and the height of the base is 12 cm.
Calculate the size of the interior angles and the length of the base of the isosceles triangle if the arm's length is 17 cm and the height of the base is 12 cm. - Trapezoid 82216
 Given is an isosceles trapezoid ABCD with bases 10 cm and 14 cm. The height of the trapezoid is 6 cm. Determine the interior angles of the trapezoid.
Given is an isosceles trapezoid ABCD with bases 10 cm and 14 cm. The height of the trapezoid is 6 cm. Determine the interior angles of the trapezoid. - Isosceles 7661
 The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles.
The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles. - Calculate triangle
 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and areas if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and areas if given a=40cm, b=57cm, and c=59cm. - Triangles
 Find out whether the given sizes of the angles can be interior angles of a triangle: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3'
Find out whether the given sizes of the angles can be interior angles of a triangle: a) 23°10',84°30',72°20' b) 90°,41°33',48°37' c) 14°51',90°,75°49' d) 58°58',59°59',60°3' - Isosceles 2588
 Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - IS triangle
 Calculate the interior angles of the isosceles triangle with base 12 cm and legs 19 cm long.
Calculate the interior angles of the isosceles triangle with base 12 cm and legs 19 cm long.
