Square practice problems - page 136 of 150
Number of problems found: 2994
- Trapezoid RT
 The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con
The plot is a rectangular trapezium ABCD, where ABIICD has a right angle at the vertex B side and AB has a length of 36 m. The lengths of the sides AB and BC are in the ratio 12:7. The lengths of the sides AB and CD are in the ratio 3:2. Calculate the con - Pyramid
 The pyramid has a base a = 2cm and height in v = 7 cm. a) calculate the angle between plane ABV and the base plane b) Calculate the angle between the edges on the opposite side.
The pyramid has a base a = 2cm and height in v = 7 cm. a) calculate the angle between plane ABV and the base plane b) Calculate the angle between the edges on the opposite side. - Corresponding 5646
 The parquet floors in the room have the shape of a rhombus with a side of 2.3 dm long and a corresponding height of 0.9 dm long. How many square meters does the room have if its floor comprises 580 parquets?
The parquet floors in the room have the shape of a rhombus with a side of 2.3 dm long and a corresponding height of 0.9 dm long. How many square meters does the room have if its floor comprises 580 parquets? - A plane vs. sphere
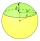 The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere.
The intersection of a plane is 2 cm from the sphere's center, and this sphere is a circle whose radius is 6 cm. Calculate the surface area and volume of the sphere. - Square pyramid
 Calculate the pyramid's volume with the side 5 cm long and with a square base, and the side base has an angle of 60 degrees.
Calculate the pyramid's volume with the side 5 cm long and with a square base, and the side base has an angle of 60 degrees. - The tent
 The tent shape of a regular quadrilateral pyramid has a base edge length of a = 2 m and a height of v = 1.8 m. If we have to add 7% of the seams, how many m² of cloth did we need to make the tent? How many m³ of air will be in the tent?
The tent shape of a regular quadrilateral pyramid has a base edge length of a = 2 m and a height of v = 1.8 m. If we have to add 7% of the seams, how many m² of cloth did we need to make the tent? How many m³ of air will be in the tent? - A rectangle 5
 A rectangle has sides of 10 cm and 14 cm. Calculate the angle between a diagonal and a long side.
A rectangle has sides of 10 cm and 14 cm. Calculate the angle between a diagonal and a long side. - Center of line segment
 Calculate the distance of point X [1,3] from the center of the line segment x = 2-6t, y = 1-4t; t is from interval <0,1>.
Calculate the distance of point X [1,3] from the center of the line segment x = 2-6t, y = 1-4t; t is from interval <0,1>. - Midpoint of segment
 Find the distance and midpoint between A(1,2) and B(5,5).
Find the distance and midpoint between A(1,2) and B(5,5). - A cylinder
 A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm?
A cylinder 108 cm high has a circumference of 24 cm. A string makes exactly six complete turns around the cylinder while its two ends touch the top and bottom. (forming a spiral around the cylinder). How long is the string in cm? - Quadrilateral shelter
 The shelter has the shape of a regular quadrilateral pyramid without a front wall. The length of the base edge is 3 meters, and the shelter's height is 3.5 meters. How much canvas must be bought to sew it if we have to increase consumption by 20% for fold
The shelter has the shape of a regular quadrilateral pyramid without a front wall. The length of the base edge is 3 meters, and the shelter's height is 3.5 meters. How much canvas must be bought to sew it if we have to increase consumption by 20% for fold - Horizon
 The top of a lighthouse is 18 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.]
The top of a lighthouse is 18 m above the sea. How far away is an object just "on the horizon"? [Assume the Earth is a sphere of radius 6378.1 km.] - Parallelogram 82695
 Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals.
Given is the parallelogram KLMN, in which we know the side sizes/KL/ = a = 84.5 cm, /KN/ = 47.8 cm, and the angle size at the vertex K 56°40'. Calculate the size of the diagonals. - Triangular pyramid
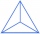 A regular tetrahedron is a triangular pyramid whose base and walls are identical equilateral triangles. Calculate the height of this body if the edge length is a = 8 cm.
A regular tetrahedron is a triangular pyramid whose base and walls are identical equilateral triangles. Calculate the height of this body if the edge length is a = 8 cm. - Glass mosaic
 How many dm² glasses are necessary to produce 97 slides of a regular 6-gon, whose side has a length of 21 cm? Assume that cutting glass waste is 10%.
How many dm² glasses are necessary to produce 97 slides of a regular 6-gon, whose side has a length of 21 cm? Assume that cutting glass waste is 10%. - Rhombus - ratio
 In a rhombus, the ratio of the side to the height to this side is 4 : 1, if its area is 49 cm². Calculate the size of the side and the height to this side.
In a rhombus, the ratio of the side to the height to this side is 4 : 1, if its area is 49 cm². Calculate the size of the side and the height to this side. - Hexagon, hexa S, V
 What is the surface area and volume of a regular hexagonal prism with a base edge of 12cm and a height of the prism equal to the diameter of the circle circumscribed by the base?
What is the surface area and volume of a regular hexagonal prism with a base edge of 12cm and a height of the prism equal to the diameter of the circle circumscribed by the base? - Hip-roof
 The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar
The roof consists of two isosceles trapezoids and two isosceles triangles. The roof plan is a rectangle with dimensions of 8m and 14m, and the roof ridge is 8m long. The height of the trapezoid is 5m, the height of the triangles is 4.2m. How many tiles ar - Masquerade ball
 Marie wants to make a cone-shaped witch's hat for a masquerade ball. How much material will it need if it counts on an annular rim with diameters of 28cm and 44cm? The hat side length is 30cm. Add 5% of the material to the bust. Round to cm².
Marie wants to make a cone-shaped witch's hat for a masquerade ball. How much material will it need if it counts on an annular rim with diameters of 28cm and 44cm? The hat side length is 30cm. Add 5% of the material to the bust. Round to cm². - ABCDEFGH 82499
 In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG?
In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
