Square practice problems - page 33 of 150
Number of problems found: 2994
- Square side
 If we enlarge the square side a = 5m, its area will increase by 10,25%. How much percent will the side of the square increase? How many percent will it increase the circumference of the square?
If we enlarge the square side a = 5m, its area will increase by 10,25%. How much percent will the side of the square increase? How many percent will it increase the circumference of the square? - Identical 6406
 The area of 90000 m² is divided into 36 identical squares. Find the length of the side of one square (in meters).
The area of 90000 m² is divided into 36 identical squares. Find the length of the side of one square (in meters). - Mechanical energy
 A stone with a mass of 2 kg falls in free fall from a tower with a height of 80 m. What is its kinetic energy, and what is its potential energy: a) At the beginning of the fall, b) In 1 s from the beginning of the fall, c) Upon impact, d) What is its mech
A stone with a mass of 2 kg falls in free fall from a tower with a height of 80 m. What is its kinetic energy, and what is its potential energy: a) At the beginning of the fall, b) In 1 s from the beginning of the fall, c) Upon impact, d) What is its mech - The projectile
 The projectile was fired horizontally from a height of h = 25 meters above the ground at a speed of v0 = 250 m/s. Find the range and flight time of the projectile.
The projectile was fired horizontally from a height of h = 25 meters above the ground at a speed of v0 = 250 m/s. Find the range and flight time of the projectile. - A tile
 A tile setter is covering a 5ft by 5ft square shower wall. Each tile covers 4 5/8in by 4 5/8in a square. How many rows of tile are needed to reach 5ft? How many tiles are needed to cover 5ft by 5ft square
A tile setter is covering a 5ft by 5ft square shower wall. Each tile covers 4 5/8in by 4 5/8in a square. How many rows of tile are needed to reach 5ft? How many tiles are needed to cover 5ft by 5ft square - Non-woven fabric
 A square sandpit should have a side length of 1.6 m. How long do you need a wooden board to enclose the sandpit? Under the sandbox, a non-woven fabric will extend by 0.2 m on each side. How much will we need?
A square sandpit should have a side length of 1.6 m. How long do you need a wooden board to enclose the sandpit? Under the sandbox, a non-woven fabric will extend by 0.2 m on each side. How much will we need? - Variability
 In the table below, the number of wrong produced goods in two shifts: morning shift: 2; 0; 6; 10; 2; 2; 4; 2; 5; 2; afternoon shift: 4; 4; 0; 2; 10; 2; 6; 2; 3; 10; Compare the variability in both shifts, compare the average number of wrong goods on both
In the table below, the number of wrong produced goods in two shifts: morning shift: 2; 0; 6; 10; 2; 2; 4; 2; 5; 2; afternoon shift: 4; 4; 0; 2; 10; 2; 6; 2; 3; 10; Compare the variability in both shifts, compare the average number of wrong goods on both - Coins
 Edmund had saved a certain number of 0.5-euro coins. He placed the coins in a single layer in a square. He had 4 coins left. When he wanted to build a square with one more row, he was missing 23 coins. How many euros does he have?
Edmund had saved a certain number of 0.5-euro coins. He placed the coins in a single layer in a square. He had 4 coins left. When he wanted to build a square with one more row, he was missing 23 coins. How many euros does he have? - Perimeter 24701
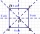 The sales stand floor plan consists of squares and has an area of 48 m². What is the perimeter of these booths? a. 34 m b. 36 m c. 40 m d. 44 m
The sales stand floor plan consists of squares and has an area of 48 m². What is the perimeter of these booths? a. 34 m b. 36 m c. 40 m d. 44 m - Rectangular 82582
 We have to pave the smallest possible square with rectangular tiles with 168 cm and 280 cm sides. What will its side of the square be?
We have to pave the smallest possible square with rectangular tiles with 168 cm and 280 cm sides. What will its side of the square be? - Distribution 73724
 The distribution of the random variable X is given in the following table. Calculate P[X is odd], E[X] and P[1<X≤6] Probability distribution table: xi; 1; 2; 3 ; 4; 5; 6; 7; 8; 9 pi; 0.30; 0.12; 0.18; 0.10; 0.07; 0.07; 0.06; 0.05; 0.05
The distribution of the random variable X is given in the following table. Calculate P[X is odd], E[X] and P[1<X≤6] Probability distribution table: xi; 1; 2; 3 ; 4; 5; 6; 7; 8; 9 pi; 0.30; 0.12; 0.18; 0.10; 0.07; 0.07; 0.06; 0.05; 0.05 - Czechoslovakia - area
 Slovakia has an area 38% smaller than the Czech Republic. Original Czechoslovakia had an area of 128,000 square kilometers. What are the areas of both states?
Slovakia has an area 38% smaller than the Czech Republic. Original Czechoslovakia had an area of 128,000 square kilometers. What are the areas of both states? - Profit growth
 A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years.
A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years. - Two gardeners
 The garden, with an area of 81 square meters, was divided by two gardeners in a ratio of 4:5. How much did the second gardener get more than the first?
The garden, with an area of 81 square meters, was divided by two gardeners in a ratio of 4:5. How much did the second gardener get more than the first? - Plastered 2529
 The mason was to plaster 24.2 m² of the wall in 12 shifts. At what percentage did he meet the plan when plastering 306 m² of walls?
The mason was to plaster 24.2 m² of the wall in 12 shifts. At what percentage did he meet the plan when plastering 306 m² of walls? - SKMO
 Petra had written natural numbers from 1 to 9. She added two of these numbers, deleted them, and wrote the resulting sum instead of the summaries. She thus had eight numbers written down, which she managed to divide into two groups with the same product.
Petra had written natural numbers from 1 to 9. She added two of these numbers, deleted them, and wrote the resulting sum instead of the summaries. She thus had eight numbers written down, which she managed to divide into two groups with the same product. - Population variance
 60% of students at a California community college will transfer to a college in the CSU system. The number of students in a sample who will transfer follows a binomial distribution. If eight students are randomly selected, find the population variance σ²
60% of students at a California community college will transfer to a college in the CSU system. The number of students in a sample who will transfer follows a binomial distribution. If eight students are randomly selected, find the population variance σ² - Chi square
 A phone battery manufacturer claims that his battery lives are approximately normally distributed with a standard deviation equal to 0.9 years. Suppose a random sample of 10 of these batteries has a standard deviation of 1.2 years. Do you think that the s
A phone battery manufacturer claims that his battery lives are approximately normally distributed with a standard deviation equal to 0.9 years. Suppose a random sample of 10 of these batteries has a standard deviation of 1.2 years. Do you think that the s - Squares ratio
 The first square has a side length of a = 6 cm. The second square has a circumference of 6 dm. Calculate the proportions of the perimeters and the proportions of these squares. (Write the ratio in the basic form). (Perimeter = 4 * a, area S = a²)
The first square has a side length of a = 6 cm. The second square has a circumference of 6 dm. Calculate the proportions of the perimeters and the proportions of these squares. (Write the ratio in the basic form). (Perimeter = 4 * a, area S = a²) - Two mass points
 Two mass points start moving simultaneously in the same direction from the same location: the first point uniformly with a speed of 50 cm/s, and the second point uniformly accelerated with zero initial speed and an acceleration of 10 cm/s². Determine a) t
Two mass points start moving simultaneously in the same direction from the same location: the first point uniformly with a speed of 50 cm/s, and the second point uniformly accelerated with zero initial speed and an acceleration of 10 cm/s². Determine a) t
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
