Quadratic function
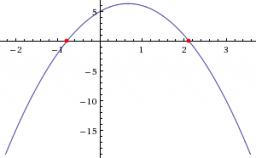
It is given a quadratic function y = -4x2+5x+c with an unknown coefficient c. Determine the smallest integer c for which the graph of f intersects the x-axis at two different points.
Final Answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
You need to know the following knowledge to solve this word math problem:
algebrabasic operations and conceptsnumbersGrade of the word problem
Related math problems and questions:
- Intersections 62784
A quadratic function is given: y = -x² + 2x + 3 a) determine the intersections with the x, y-axis and peak V b) draw a graph and describe c) for which x applies f (x) = 3 - General line equations
In all examples, write the GENERAL EQUATION OF a line that is given in some way. A) the line is given parametrically: x = - 4 + 2p, y = 2 - 3p B) the slope form gives the line: y = 3x - 1 C) the line is given by two points: A [3; -3], B [-5; 2] D) the lin - A Cartesian framework
1. In a Cartesian framework, the functions f and g we know that: The function (f) is defined by f (x) = 2x², the function (g) is defined by g (x) = x + 3, the point (O) is the origin of the reference, and point (C) is the point of intersection of the grap - Intersection of functions
Draw a graph of the function given by the equation y = -2x +3, find its intersections with the coordinate axes, and complete the unknown coordinates A [3;? ], B [?; 8]. - Quadratic function 2
Which of the points belong to function f:y= 2x²- 3x + 1 : A(-2, 15) B (3,10) C (1,4) - Determine 6621
1) The function f is given: y = I 2-x I + 2. Determine the values of the function in points, i.e., F (-2), f (0), f (1), f (4,8). - Line intersect segment
Decide whether the line p : x + 2 y - 7 = 0 intersects the line segment given by points A[1, 1] and B[5, 3]
