Triangle practice problems - page 6 of 125
Number of problems found: 2496
- A lamp
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - X-triangle
Find the length of the x segment in the given triangle drawings. - Three inscribed objects
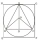A circle is inscribed in a square. An equilateral triangle of side 4√3 is inscribed in that circle. Find the length of the diagonal of the square. - The apothem
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - PQR - Euclid
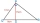Find the length of line segment PR - leg of the right triangle PQR. PQ=17 cm PS=15 cm QS=8 cm; Point S is the height touch point with a hypotenuse of the RQ. - Two chords 2
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm away from the center of the circle, calculate the length of the second chord. - Line segment
Find the length of the line joining points A(-4,8) and B(-1,4). - Parallelogram - right angles
In parallelogram ABCD; AB = 16 cm, BC = 12 cm and diagonal AC = 20 cm. Find the area of the parallelogram. - Four points
There are 4 nonlinear points. How many triangles can form by joining them? - Two chords 6 A chord PQ is 10.4cm long, and its distance from the center of a circle is 3.7cm. Calculate the length of a second chord RS, which is 4.1cm from the center of this circle.
- A chord 2
A chord of length 16 cm is drawn in a circle of radius 10 cm. Calculate the distance of the chord from the center of the circle. - The volume 8
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Slant height 3
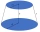The frustum of a right circular cone has the diameters of base 10 cm of top 6 cm and a height of 5 cm. Find the slant height. - A triangle 3
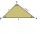A triangle has a base of 5 5/6 feet and a height of 7 2/5 feet. Find the area of the triangle as a mixed number. - Calculate roots of z
Calculate the ratio of the two fifth roots of the number 32. - Area of a triangle
Find the area of a triangle with a base of 7 mm and a height of 10 mm. - Center traverse
Does the middle traverse indeed bisect the triangle? - Identical 32703
How many identical triangles do the middle bars divide the triangle ▲? - An isosceles 2
An isosceles triangular frame has a measure of 72 meters on its legs and 18 meters on its base. Find the perimeter of the frame. - The perimeter
The perimeter of the triangle is 24, and the sides are integers and form an arithmetic sequence. Specify the side sizes of this triangle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
