Triangle practice problems - page 7 of 126
Number of problems found: 2501
- Midpoints
 Triangle whose sides are midpoints of sides of triangle ABC has a perimeter 83. How long is the perimeter of the triangle ABC?
Triangle whose sides are midpoints of sides of triangle ABC has a perimeter 83. How long is the perimeter of the triangle ABC? - Identical 32703
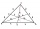 How many identical triangles do the middle bars divide the triangle ▲?
How many identical triangles do the middle bars divide the triangle ▲? - An isosceles 2
 An isosceles triangular frame has a measure of 72 meters on its legs and 18 meters on its base. Find the perimeter of the frame.
An isosceles triangular frame has a measure of 72 meters on its legs and 18 meters on its base. Find the perimeter of the frame. - The perimeter
 The perimeter of the triangle is 24, and the sides are integers and form an arithmetic sequence. Specify the side sizes of this triangle.
The perimeter of the triangle is 24, and the sides are integers and form an arithmetic sequence. Specify the side sizes of this triangle. - Scalene triangle
 Solve the triangle: A = 50°, b = 13, c = 6
Solve the triangle: A = 50°, b = 13, c = 6 - Angle
 Draw angle |∠ ABC| = 30° and build its axis. What angle is between the axis angle and arm of angle?
Draw angle |∠ ABC| = 30° and build its axis. What angle is between the axis angle and arm of angle? - Calculate 4013
 In a triangle, one internal angle measures 36 degrees. The second angle is twice the third angle. Calculate unknown angles.
In a triangle, one internal angle measures 36 degrees. The second angle is twice the third angle. Calculate unknown angles. - The angles
 The angles in the triangle are in the ratio 12:15:9. Find the angles.
The angles in the triangle are in the ratio 12:15:9. Find the angles. - Identical line
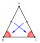
 In which triangles is the line identical with the height?
In which triangles is the line identical with the height? - 3-bracket 2
 Maybe the smallest angle in the triangle is greater than 70°?
Maybe the smallest angle in the triangle is greater than 70°? - 3-bracket
 Maybe the largest angle in the triangle is less than 20°?
Maybe the largest angle in the triangle is less than 20°? - Third interior angle
 Find the third interior angle of the triangle ABC where: α = 48°, γ = 65°.
Find the third interior angle of the triangle ABC where: α = 48°, γ = 65°. - Possible lengths
 Find the possible lengths for the third side of a triangle with sides 20 and 18.
Find the possible lengths for the third side of a triangle with sides 20 and 18. - Isosceles triangle
 Calculate the perimeter of the isosceles triangle with arm length 87 cm and base length of 95 cm.
Calculate the perimeter of the isosceles triangle with arm length 87 cm and base length of 95 cm. - Third angle
 What is the third angle of a triangle if the first two angles have sizes 50° and 60°?
What is the third angle of a triangle if the first two angles have sizes 50° and 60°? - Calculation - isosceles
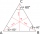 Calculate the area and perimeter of an isosceles triangle if given: base a: 6cm, height to the base: 4cm.
Calculate the area and perimeter of an isosceles triangle if given: base a: 6cm, height to the base: 4cm. - An equilateral triangle
 The perimeter of an equilateral triangle is 33cm. How long is each side?
The perimeter of an equilateral triangle is 33cm. How long is each side? - Determine 69364
 Determine the angle ϕ: ϕ + 71 ° 15 '= 90 °
Determine the angle ϕ: ϕ + 71 ° 15 '= 90 ° - Triangle 16953
 In the ABC triangle, the alpha angle is 36 degrees. The beta angle is twice the gamma. What is this triangle?
In the ABC triangle, the alpha angle is 36 degrees. The beta angle is twice the gamma. What is this triangle? - Triangular numbers
 The first four triangular numbers are 1,3,6,10. What is the 10th triangular number? Help: A triangular number or triangle number counts objects arranged in an equilateral triangle.
The first four triangular numbers are 1,3,6,10. What is the 10th triangular number? Help: A triangular number or triangle number counts objects arranged in an equilateral triangle.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
