Triangle + fractions - practice problems
Number of problems found: 204
- A triangular
 A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides?
A triangular frame has sides that measure 15’-7",20’-4", and 26’-2". What is the total length of the three sides? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - The angles
 The angles in the triangle are in the ratio 12:15:9. Find the angles.
The angles in the triangle are in the ratio 12:15:9. Find the angles. - Area of a triangle
 What is the area of a triangle that has a base of 4 1/4 and a height of 3 3/3?
What is the area of a triangle that has a base of 4 1/4 and a height of 3 3/3?
- Determine 17803
 In a triangle, the aspect ratio is a: b = 2: 1, and the aspect ratio is b: c = 3: 4. Determine the aspect ratio a: b: c.
In a triangle, the aspect ratio is a: b = 2: 1, and the aspect ratio is b: c = 3: 4. Determine the aspect ratio a: b: c. - The angles 3
 The angles in a triangle are in the ratio of 3:4:5. Work out the size of each angle.
The angles in a triangle are in the ratio of 3:4:5. Work out the size of each angle. - Perimeter+mixed
 Find the perimeter of a triangle whose sides are 5 1/2 cm, 7 3/5 cm, and 3 1/4 cm, respectively.
Find the perimeter of a triangle whose sides are 5 1/2 cm, 7 3/5 cm, and 3 1/4 cm, respectively. - Calculate 68394
 The sizes of the interior angles of the triangle are in the ratio of 3:4:5. Calculate these angles.
The sizes of the interior angles of the triangle are in the ratio of 3:4:5. Calculate these angles. - Interior angles
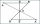 Calculate the interior angles of a triangle that are in the ratio 2:3:4.
Calculate the interior angles of a triangle that are in the ratio 2:3:4.
- Three-fifths 80366
 Calculate in cm the perimeter of a triangle with sides a, b, and c. If a is two-thirds of side b, c is three-fifths side b; b=15 cm.
Calculate in cm the perimeter of a triangle with sides a, b, and c. If a is two-thirds of side b, c is three-fifths side b; b=15 cm. - Triangle of cans
 A display of cans on a grocery shelf consists of 28 cans at the bottom, 25 cans in the next row, and so on. There are nine rows on a shelf. How many cans are there in the 9th row? How many cans in total are on display?
A display of cans on a grocery shelf consists of 28 cans at the bottom, 25 cans in the next row, and so on. There are nine rows on a shelf. How many cans are there in the 9th row? How many cans in total are on display? - Circumference 31361
 The lengths of the triangle sides are in the ratio of 3:5:7. Its circumference is 45 cm. Find its lengths.
The lengths of the triangle sides are in the ratio of 3:5:7. Its circumference is 45 cm. Find its lengths. - Bevel
 I have a bevel in the ratio 1:6. What is the angle, and how do I calculate it?
I have a bevel in the ratio 1:6. What is the angle, and how do I calculate it? - Sides in ratio
 The sides of the triangle are in a ratio of 2: 6: 5. Find the dimensions of the remaining sides if the longest side is 32 cm.
The sides of the triangle are in a ratio of 2: 6: 5. Find the dimensions of the remaining sides if the longest side is 32 cm.
- The pole
 A 4 m bullet supports the telegraph pole. It is at 3/4 of pole height, and the end is at a distance of 2.5 m from the pole post. Calculate the height of the telegraph pole.
A 4 m bullet supports the telegraph pole. It is at 3/4 of pole height, and the end is at a distance of 2.5 m from the pole post. Calculate the height of the telegraph pole. - Painters
 Six of the painters paint 90 m of the fence in five hours. For how long would the four painters paint a 45-meter fence? How many meters of the fence were painted by painters 5 for two hours?
Six of the painters paint 90 m of the fence in five hours. For how long would the four painters paint a 45-meter fence? How many meters of the fence were painted by painters 5 for two hours? - Angles ratio
 In an ABC triangle, is true relationship c is less than b, and b is less than a. Internal angles of the triangle are in the ratio 5:4:9. The size of the internal angle beta is:
In an ABC triangle, is true relationship c is less than b, and b is less than a. Internal angles of the triangle are in the ratio 5:4:9. The size of the internal angle beta is: - Perimeter 6002
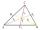 In the triangle ABC there is a side c = 5cm and a medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity).
In the triangle ABC there is a side c = 5cm and a medians ta = 6cm (median to side a), tb = 4.5cm (median to side b). Find the perimeter of the triangle ABT (T = center of gravity). - The angles ratio
 The angles in the ABC triangle are in the ratio 1:2:3. Find the angles' sizes and determine what kind of a triangle it is.
The angles in the ABC triangle are in the ratio 1:2:3. Find the angles' sizes and determine what kind of a triangle it is.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
