Physical quantity - math word problems - page 106 of 346
Number of problems found: 6908
- Two thirds 3
 Two-thirds of the money in my pocket is 50 cents. What is 1/3 of the money in my pocket?
Two-thirds of the money in my pocket is 50 cents. What is 1/3 of the money in my pocket? - The length 7
 The length of a water pipe is 7 m. How many ¼ m lengths can Jane cut from the pipe?
The length of a water pipe is 7 m. How many ¼ m lengths can Jane cut from the pipe? - Eight 9
 Eight pipes are 2¼ meters long . what is the total length of the eight pipes?
Eight pipes are 2¼ meters long . what is the total length of the eight pipes? - Difference of temperatures
 The temperature on Saturday was –2°C. The temperature on Sunday was 8°C. Write down the difference between these two temperatures.
The temperature on Saturday was –2°C. The temperature on Sunday was 8°C. Write down the difference between these two temperatures. - Storm 3
 If the temperature yesterday was 56 and Today is 13 degrees cooler, what is Today's temperature?
If the temperature yesterday was 56 and Today is 13 degrees cooler, what is Today's temperature? - Radians compare
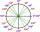 What is the greater angle? -6.6 radians or -6.6π radians?
What is the greater angle? -6.6 radians or -6.6π radians? - Angles
 Which of those angles is obtuse?
Which of those angles is obtuse? - Life
 Calculate how many years has man lived for 27869 days?
Calculate how many years has man lived for 27869 days? - Advantageous: 81060
 Determine which purchase is more advantageous: ... ...
Determine which purchase is more advantageous: ... ... - The low 2
 The low temperature on Monday was –5°C. On Tuesday, the low temperature was 3 degrees warmer than on Monday. What was the low temperature on Tuesday?
The low temperature on Monday was –5°C. On Tuesday, the low temperature was 3 degrees warmer than on Monday. What was the low temperature on Tuesday? - Yesterday
 Yesterday the temperature was 24.5°C. Today, the temperature has dropped by 5°C. What is the temperature today?
Yesterday the temperature was 24.5°C. Today, the temperature has dropped by 5°C. What is the temperature today? - Half of the recipe
 A recipe for a pancake needs 3 1/4 cups of flour. How much flour is needed to make half of the recipe?
A recipe for a pancake needs 3 1/4 cups of flour. How much flour is needed to make half of the recipe? - A kilogram
 A kilogram of pork is P50. How much is 1/4 of it?
A kilogram of pork is P50. How much is 1/4 of it? - A shopkeeper 2
 A shopkeeper charged E17 for four textbooks of the same kind. What is the cost of one textbook?
A shopkeeper charged E17 for four textbooks of the same kind. What is the cost of one textbook? - Lenth - meter
 Find in centimeters, 3/10 of a half meter.
Find in centimeters, 3/10 of a half meter. - The temperature 2
 The temperature of Siberia fell 13 degrees below 2/3 degrees Celsius. What is the temperature there now?
The temperature of Siberia fell 13 degrees below 2/3 degrees Celsius. What is the temperature there now? - Change in temperature
 The starting temperature is 21°C, and the highest temperature is 32°C. What is the change in temperature?
The starting temperature is 21°C, and the highest temperature is 32°C. What is the change in temperature? - 8 degrees
 Eight degrees Celsius, then cools down by 9 degrees Celsius. What is the resultant temperature?
Eight degrees Celsius, then cools down by 9 degrees Celsius. What is the resultant temperature? - Weeks
 22 weeks is equal to how many days?
22 weeks is equal to how many days? - Doctors
 In the city operates 75 doctors. The city has 43650 citizens. How many citizens are per doctor?
In the city operates 75 doctors. The city has 43650 citizens. How many citizens are per doctor?
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
