Physical quantity - math word problems - page 157 of 344
Number of problems found: 6862
- Work
Workers work five days a week and have 28 days of vacation a year. Calculate how many days is out of work and express it as a percentage. Consider that a year has 52 weeks. - Segments
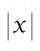Which of the pairs of numbers on the number line encloses the longest segment: ... - Fraction 26291
Write the per mille as a fraction Seven ‰ 25 ‰ 15 ‰ 10 ‰ 2.5 ‰ 1.7 ‰ 0.8 ‰ 2 ‰ - Percentage 3892
The bar contains 81g of coconut per 200g. What percentage of coconut does the bar have? - Commission 83406
The purchase price of the material is 1000 CZK, and the margin is 35%. What will be the selling price? This is not a trademark or commission. - Deciliters 82303
Juraj had 1 liter of pure orange juice in the bottle. He drained 2 deciliters of it and replaced it with water. What is the ratio of orange juice to water in the bottle now? - Yesterday 79344
Petr played Minecraft for 2 hours yesterday. Pavel played 10% longer. How many minutes did Pavel play? - The temperature 18
The temperature at 12:00 PM was 43°F. Over the day, the temperature decreased by 3.5°F per hour. What was the new temperature at 6:00 PM? - Percentage 6695
By what percentage is the volume of the first container larger than the volume of the second when the first container has 70 liters and the second 36 liters? - Principal 6066
After a year, little Katka was on a passbook of thousands of euros. What was the annual interest rate in the bank, and the principal was 957 euros? - Spending
Suppose I spend 25% of my net pay of $922.28 on entertainment. How much money is that? - Calculate 3996
The initial share price first fell by 2%, and then this new price rose by 20%. The final share price is CZK 2,400. Calculate the initial share price. - Workers 3235
Eight workers in 6 days sweep 2400 m² roads. How many m² will six workers clean in 4 days? - Original 2739
Dresses on sale have become cheaper twice: first by 12%, then by 25% of the new price. What% of the original price was the final price? - Backpack
A large backpack costs CZK 1352. Little is 35% cheaper. How much do we pay for five large and two small backpacks? - Expensive 1636
A pound of Idared apples costs 34 cents. How many euros does 7 kg of three times more expensive Jonagold apples cost? - Luminosity 1575
Ten lamps with a certain luminosity are needed to illuminate the rooms. How many lamps with 2.5 times more brightness are needed for the same lighting in the same room? - Monthly payments
Novákovi pays for electricity, and monthly pays at the end of the year still bill 25 Euro. Total per year pay 512 Euro. What were their monthly payments? - Frightened 7734
A frightened ant runs along a 16 cm long ruler at a constant speed of 1 cm per second. He always turns around and runs back after reaching the end of the ruler. Each turn takes 1 second. He started running from the left corner. Next, how many numbers will - Additional 7569
The store reduced the original price by 40% during the sale. In addition, he sent an SMS message to his loyal customers with an offer of an additional 15% discount on the price of already discounted goods. Calculate how much the original price was reduced
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
