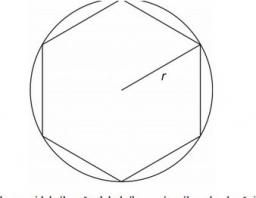
Hexagon A
Calculate the area of a regular hexagon inscribed in a circle with radius r=9 cm.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Calculate 25621
 Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm.
Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm. - Hexagon
 Draw a regular hexagon inscribed in a circle with a radius r=8 cm. What is its perimeter?
Draw a regular hexagon inscribed in a circle with a radius r=8 cm. What is its perimeter? - Inscribed 7018
 The dragon has the shape of a regular hexagon inscribed in a circle with a radius of 20 cm. What is the area of the dragon?
The dragon has the shape of a regular hexagon inscribed in a circle with a radius of 20 cm. What is the area of the dragon? - Circle and hexagon
 Calculate the radius of a circle whose circumference is 8.4 cm longer than the inscribed regular hexagon's circumference.
Calculate the radius of a circle whose circumference is 8.4 cm longer than the inscribed regular hexagon's circumference.
- Hexagon in circle
 Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle.
Calculate the radius of a circle whose length is 10 cm greater than the circumference of a regular hexagon inscribed in this circle. - Nine-gon
 Calculate the perimeter of a regular nonagon (9-gon) inscribed in a circle with a radius 13 cm.
Calculate the perimeter of a regular nonagon (9-gon) inscribed in a circle with a radius 13 cm. - Pentagon
 Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm.
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm. - Circumscribed 7290
 Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm.
Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm. - Nine-sided 36071
 Calculate the surface area and volume of a regular nine-sided pyramid if the radius of the circle inscribed in the base measures ρ = 12 cm and the height of the pyramid is 24 cm
Calculate the surface area and volume of a regular nine-sided pyramid if the radius of the circle inscribed in the base measures ρ = 12 cm and the height of the pyramid is 24 cm
- Office
 The office building was built in the shape of a regular hexagon inscribed in a circle with a radius of 12 m. The height of the walls is 7m. How much does CZK cost plastering the walls of the building if per 1 m square costs CZK 400?
The office building was built in the shape of a regular hexagon inscribed in a circle with a radius of 12 m. The height of the walls is 7m. How much does CZK cost plastering the walls of the building if per 1 m square costs CZK 400? - Difference 80618
 A regular hexagon is described and inscribed in a circle. The difference between its areas is 8√3. Find the circle's radius.
A regular hexagon is described and inscribed in a circle. The difference between its areas is 8√3. Find the circle's radius. - Pentadecagon
 Calculate the area of a regular 15-sides polygon inscribed in a circle with a radius r = 4. Express the result to two decimal places.
Calculate the area of a regular 15-sides polygon inscribed in a circle with a radius r = 4. Express the result to two decimal places. - Hexagonal pyramid
 Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm.
Calculate the surface area of a regular hexagonal pyramid with a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. - Hexagonal 13891
 A regular hexagonal pyramid has a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. Please sketch the picture. Please calculate the surface of a regular hexagonal pyramid.
A regular hexagonal pyramid has a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. Please sketch the picture. Please calculate the surface of a regular hexagonal pyramid.
- Calculate 16223
 The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle).
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Regular n-gon
 Which regular polygon has a radius of circumscribed circle r = 10 cm and the radius of inscribed circle p = 9.962 cm?
Which regular polygon has a radius of circumscribed circle r = 10 cm and the radius of inscribed circle p = 9.962 cm? - Diagonals of pentagon
 Calculate the diagonal length of the regular pentagon: a) inscribed in a circle of radius 12dm; b) a circumscribed circle with a radius of 12dm.
Calculate the diagonal length of the regular pentagon: a) inscribed in a circle of radius 12dm; b) a circumscribed circle with a radius of 12dm.
