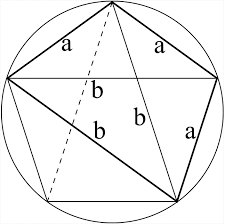
Diagonals of pentagon

Calculate the diagonal length of the regular pentagon:
a) inscribed in a circle of radius 12 dm;
b) a circumscribed circle with a radius of 12 dm.

Your answer:

Help us improve! If you spot a mistake, please let let us know. Thank you!

Tips for related online calculators

See also our right triangle calculator.
See also our trigonometric triangle calculator.

You need to know the following knowledge to solve this word math problem:

algebra

rearrange variables

planimetry

right triangle
circle
polygon
area of a shape
triangle
diagonal

goniometry and trigonometry

sine
cosine
tangent

Units of physical quantities

angle

Grade of the word problem

high school

We encourage you to watch this tutorial video on this math problem: video1

Related math problems and questions:

Inscribed and described circle
Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm.
Circumscription
Calculate the radius of the circumscribed circle of a rectangle with sides 3 and 6. Can a circle be inscribed in a rectangle?
Pentagon
Calculate the length of a regular pentagon's side, circumference, and area, inscribed in a circle with a radius r = 6 cm.
Circumscribed decagon
In a regular decagon, the diameter of the circumscribed circle measures 10 cm. Determine the radius of the circle inscribed in this decagon.
Regular n-gon
Which regular polygon has a circumscribed circle radius of r = 10 cm and an inscribed circle radius of p = 9.962 cm?
Circles
The area of a circle inscribed in a square is 7. What is the area of a circle circumscribed around a square?
Truncated cone 6
Calculate the volume of the truncated cone whose bases consist of an inscribed circle and a circle circumscribed to the opposite sides of the cube with the edge length a=1.