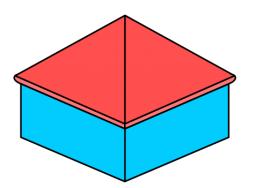
House roof
The house's roof is a regular quadrangular pyramid with a base edge 20 m. If the roof pitch is 38° and we calculate 12% of waste, connections, and overlapping of the area roof, how much m2 is needed to cover the roof?
Final Answer:
Tips for related online calculators
Our percentage calculator will help you quickly and easily solve a variety of common percentage-related problems.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
solid geometryplanimetricsbasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Four-sided 27601
 The house's roof has the shape of a regular four-sided pyramid 4 m high with a base edge of 100 dm. We consider 30% of the roofing in addition to the overlap. Calculate how much m² of roofing is needed to cover the roof.
The house's roof has the shape of a regular four-sided pyramid 4 m high with a base edge of 100 dm. We consider 30% of the roofing in addition to the overlap. Calculate how much m² of roofing is needed to cover the roof. - The roof
 The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste.
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - Regular quadrangular pyramid
 How many square meters are needed to cover the shape of a regular quadrangular pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%.
How many square meters are needed to cover the shape of a regular quadrangular pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%. - Roof 7
 The roof is a regular quadrangular pyramid with a base edge of 12 m, and a height of 4 m. How many percent is folds and waste if in construction was consumed 181.4m² of the plate was?
The roof is a regular quadrangular pyramid with a base edge of 12 m, and a height of 4 m. How many percent is folds and waste if in construction was consumed 181.4m² of the plate was? - The roof
 The house's roof has the shape of a regular quadrilateral pyramid 5 m high and the edge of the base 7 m. How many tiles with an area of 540 cm² are needed?
The house's roof has the shape of a regular quadrilateral pyramid 5 m high and the edge of the base 7 m. How many tiles with an area of 540 cm² are needed? - Roof cover
 Above the pavilion with a square ground plan with a side length of a = 12 m is a pyramid-shaped roof with a height v = 4.5 m. Calculate how much m² of sheet metal is needed to cover this roof; if 5.5% of the sheet, we must add for joints and waste.
Above the pavilion with a square ground plan with a side length of a = 12 m is a pyramid-shaped roof with a height v = 4.5 m. Calculate how much m² of sheet metal is needed to cover this roof; if 5.5% of the sheet, we must add for joints and waste. - Four-sided turret
 The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste?
The turret has the shape of a regular four-sided pyramid with a base edge 0.8 m long. The height of the turret is 1.2 m. How many square meters are needed to cover it, counting the extra 10% sheet metal waste?
