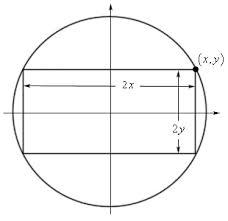
Inscribed rectangle
The circle area is 231. Determine the area of the inscribed rectangle with one side 13 long.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsGrade of the word problem
Related math problems and questions:
- Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Square inscribed
 Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm.
Find the length of the side of the square ABCD, which is inscribed to a circle k with a radius of 10 cm. - Infinity
 A square with a side 19 long is an inscribed circle, and the circle is inscribed next to the square, circle, and so on to infinity. Calculate the sum of the area of all these squares.
A square with a side 19 long is an inscribed circle, and the circle is inscribed next to the square, circle, and so on to infinity. Calculate the sum of the area of all these squares. - Dimensions 82414
 The flag of Brazil has a yellow diamond on a green field with a blue circle inside. If we had a flag with dimensions of 70 cm x 50 cm, the rhombus would have a side 35 cm long and a height of 30 cm. Indicate with fractions in basic form what part of the f
The flag of Brazil has a yellow diamond on a green field with a blue circle inside. If we had a flag with dimensions of 70 cm x 50 cm, the rhombus would have a side 35 cm long and a height of 30 cm. Indicate with fractions in basic form what part of the f - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Quatrefoil
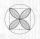 Calculate the quatrefoil area, inscribed in a square with a side of 6 cm.
Calculate the quatrefoil area, inscribed in a square with a side of 6 cm. - Difference 66354
 A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle.
A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle.
