Cathethus and the inscribed circle
A right triangle is given one leg long 14 cm and the radius of the inscribed circle of 5 cm. Calculate the area of this right triangle.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- RT = legs, circle
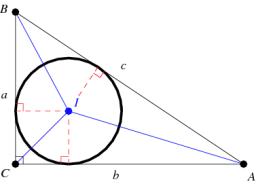
One leg of a right triangle ABC has length a= 14 cm and the radius of the circle inscribed in this triangle r= 5 cm. Calculate the length of the hypotenuse and its other leg. - Triangle circle radius
Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle. - Circle described
The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle. - Hexagon area calculation
Calculate the area of a regular hexagon inscribed in a circle with a radius r = 7 cm. - Right triangle
A circle with a radius of 5 cm is described in a right triangle with a 6 cm leg. What is the height at the hypotenuse of this triangle? - Inscribed circle
The circle inscribed in a triangle has a radius of 3 cm. Express the area of the triangle using a, b, and c. - Hexagon A
Calculate the area of a regular hexagon inscribed in a circle with radius r=15 cm.
