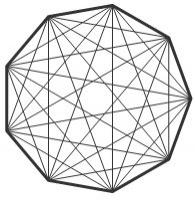
N-gon
How many diagonals does a convex 30-gon have?
Final Answer:
Tips for related online calculators
Would you like to compute the count of combinations?
See also our permutations calculator.
See also our variations calculator.
See also our permutations calculator.
See also our variations calculator.
You need to know the following knowledge to solve this word math problem:
combinatoricsplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- N-gon angles
What is the sum of interior angles 8-gon? What is the internal angle of a regular convex 8-polygon? - Diagonals
What x-gon has 54 diagonals? - Hexagon diagonal count
Does a hexagon have 275 diagonals? - Polygon Diagonals Sides
The number of diagonals of a given polygon is 88 more than the number of its sides. How many sides does this polygon have - Octagon area
An irregular convex octagon is inscribed in the circle. Its four adjacent sides have a length of 3, and the remaining four adjacent sides have a size of 2. What is the area of a given octagon? - Square diagonal construction
There are three different points, C, E, and F, in the plane. Please draw the square ABCD when E and F lie on the diagonals of this square. How many solutions does the task have? Thank you - 4-gon
Is it true that a 4-gon whose two sides are parallel and the other two have equal length is a parallelogram?
