Internal angles
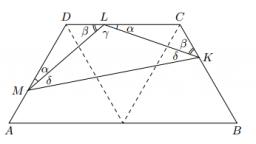
The ABCD is an isosceles trapezoid, which holds:
|AB| = 2 |BC| = 2 |CD| = 2 |DA|:
On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Determine the internal angles of the KLM triangle.
|AB| = 2 |BC| = 2 |CD| = 2 |DA|:
On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Determine the internal angles of the KLM triangle.
Final Answer:
Showing 1 comment:
Math student
Help. First, look at the inner angles of the ABCD trapezoid.
Solution. It follows from the assumptions that the center line of the AB segment with the vertices C and D divides the ABCD trapezoid into three identical equilateral triangles. Therefore, the magnitude of internal angles in the trapezoid at A and B vertices is equal to 60 °
And at the C and D vertices 120 °. It follows from the specification that the triangles LCK and MDL are the same (according to the sentence above). Therefore, both the KL and LM lines and the designated pairs of angles are the same; The magnitudes of these angles are denoted α and β. The triangle KLM is isosceles and the angles at the base are the same; Their size is denoted by δ and the size of the angle KLM is denoted by γ.
From the sum of the inner angles in the KCL triangle we derive
α + β = 180° − 120° = 60°
The sum of the three marked angles with the vertex L is a straight angle, therefore
γ = 180° − (α + β) = 120°
Finally, we deduce the sum of inner angles in the triangle KLM
δ = (180° − 120°)/2 = 30°
The internal angles of the triangle KLM are 30° and 120°
Solution. It follows from the assumptions that the center line of the AB segment with the vertices C and D divides the ABCD trapezoid into three identical equilateral triangles. Therefore, the magnitude of internal angles in the trapezoid at A and B vertices is equal to 60 °
And at the C and D vertices 120 °. It follows from the specification that the triangles LCK and MDL are the same (according to the sentence above). Therefore, both the KL and LM lines and the designated pairs of angles are the same; The magnitudes of these angles are denoted α and β. The triangle KLM is isosceles and the angles at the base are the same; Their size is denoted by δ and the size of the angle KLM is denoted by γ.
From the sum of the inner angles in the KCL triangle we derive
α + β = 180° − 120° = 60°
The sum of the three marked angles with the vertex L is a straight angle, therefore
γ = 180° − (α + β) = 120°
Finally, we deduce the sum of inner angles in the triangle KLM
δ = (180° − 120°)/2 = 30°
The internal angles of the triangle KLM are 30° and 120°
8 years ago 5 Likes
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Isosceles 2588
 Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that
Given an isosceles trapezoid ABCD, in which | AB | = 2 | BC | = 2 | CD | = 2 | DA | holds. On its side BC, the point K is such that | BK | = 2 | KC |; on its CD side, the point L is such that | CL | = 2 | LD |, and on its DA side, the point M is such that - Trapezoid 4908
 Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid.
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid. - One trapezium
 One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area.
One trapezium has AB=24M, BC=36M, CD=80M, DA=80M long sides. Find the area. - Triangle ABP
 An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP.
An isosceles trapezoid ABCD is given. The length of side AB is 10 cm, the length of CD is 7 cm, and the height to side AB is 4 cm. Point P is the base of the altitude to side AD. Calculate the area of the triangle ABP. - Trapezoid: 18703
 In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle.
In the ABCD trapezoid: | AD | = | CD | = | BC | a | AB | = | AC |. Determine the size of the delta angle. - Triangle ABC
 There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - Pentagon
 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
