Rovnoramenný lichoběžník
Je dán rovnoramenný lichoběžník ABCD, v němž platí:
|AB| = 2|BC| = 2|CD| = 2|DA|:
Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL| = 2|LD|, a na jeho straně DA je bod M takový, že |DM| = 2|MA|. Určete velikosti vnitřních úhlu trojúhelníku KLM.
|AB| = 2|BC| = 2|CD| = 2|DA|:
Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL| = 2|LD|, a na jeho straně DA je bod M takový, že |DM| = 2|MA|. Určete velikosti vnitřních úhlu trojúhelníku KLM.
Správná odpověď:
Zobrazuji 1 komentář:
Mo-radce
Nápověda. Zaměřte se nejprve na vnitřní úhly lichoběžníku ABCD.
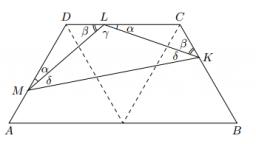
Řešení. Z předpokladů plyne, že spojnice středu úsečky AB s vrcholy C a D rozděluje lichoběžník ABCD na tři shodné rovnostranné trojúhelníky. Proto velikosti vnitřních úhlů v lichoběžníku u vrcholů A a B jsou rovny 60°
a u vrcholů C a D jsou 120°. Ze zadání dále plyne, že trojúhelníky LCK a MDL jsou shodné (podle věty sus). Proto také úsečky KL a LM a vyznačené dvojice úhlů jsou shodné; velikosti těchto úhlů označíme α a β. Trojúhelník KLM je rovnoramenný a úhly u základny jsou taktéž shodné; jejich velikost označíme δ a velikost úhlu KLM označíme γ.
Ze součtu vnitřních úhlů v trojúhelníku KCL odvodíme
α + β = 180° − 120° = 60°
Součet tří vyznačených úhlů s vrcholem L je přímý úhel, tudíž
γ = 180° − (α + β) = 120°
Konečně, ze součtu vnitřních úhlů v trojúhelníku KLM odvodíme
δ = (180° − 120°)/2 = 30°
Velikosti vnitřních úhlů trojúhelníku KLM jsou 30° a 120°
Řešení. Z předpokladů plyne, že spojnice středu úsečky AB s vrcholy C a D rozděluje lichoběžník ABCD na tři shodné rovnostranné trojúhelníky. Proto velikosti vnitřních úhlů v lichoběžníku u vrcholů A a B jsou rovny 60°
a u vrcholů C a D jsou 120°. Ze zadání dále plyne, že trojúhelníky LCK a MDL jsou shodné (podle věty sus). Proto také úsečky KL a LM a vyznačené dvojice úhlů jsou shodné; velikosti těchto úhlů označíme α a β. Trojúhelník KLM je rovnoramenný a úhly u základny jsou taktéž shodné; jejich velikost označíme δ a velikost úhlu KLM označíme γ.
Ze součtu vnitřních úhlů v trojúhelníku KCL odvodíme
α + β = 180° − 120° = 60°
Součet tří vyznačených úhlů s vrcholem L je přímý úhel, tudíž
γ = 180° − (α + β) = 120°
Konečně, ze součtu vnitřních úhlů v trojúhelníku KLM odvodíme
δ = (180° − 120°)/2 = 30°
Velikosti vnitřních úhlů trojúhelníku KLM jsou 30° a 120°
7 let 4 Likes
Tipy na související online kalkulačky
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Rovnoramenný 2588
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že|DM|= 2|MA|. Určete velikosti v - Trojúhelníku 4908
Lichoběžník ABCD se základnami AB=a, CD=c má výšku v. Bod S je střed ramene BC. Dokažte, že obsah trojúhelníku ASD se rovná polovině obsahu lichoběžníku ABCD. - Lichoběžník 21 Je dán lichoběžníku ABCD s rovnoběžnými stranami AB a CD pro bod E strany AB plati, že úsečka DE dělí lichoběžník na dvě části se stejným obsahem. Spočítej délku úsečky AE.
- Trojúhelník
V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC. - Vzdálenosti 64804
Dán je čtverec ABCD. Na jeho úhlopříčce AC leží bod E tak, že platí vzdálenost AB je rovna vzdálenosti AE. Jaká je velikost úhlu EBC? - V lichoběžníku 5
V lichoběžníku ABCD (AB II CD) je α = 57°, γ = 4β. Vypočítejte velikost všech vnitřních úhlů. - Lichoběžník 7589
Jeden lichoběžník má AB=24M, BC=36M, CD=80M, DA=80M dlouhé strany. Najděte jeho obsah. - Počet trojúhelníků
Je dán čtverec ABCD a na každé jeho straně 4 vnitřních bodů. Určete počet všech trojúhelníků s vrcholy v těchto bodech. - Pětiúhelník
Vývěsní štít má tvar pětiúhelníku ABCDE, ve kterém úsečka BC je kolmá na úsečku AB a EA je kolmá na úsečku AB. Bod P je pata kolmice spuštění z bodu D na úsečku AB. |AP|=|PB|, |BC|=|EA|=6dm, |PD|=8,4dm. Na štítu je vyznačen bod X - průsečík úseček PE a DA - V rovnoramenném 4
V rovnoramenném lichoběžníku ABCD jsou dány jeho základny AB=20cm, CD=12cm a ramena AD=BC=8cm. Určete jeho výšku a úhel alfa při vrcholu A - V čtverci
V čtverci ABCD se stranou a = 6 cm je bod E střed strany AB a bod F střed strany BC. Vypočítejte velikost všech úhlů trojúhelníku DEF a délky jeho stran. - Pětiúhelník
Uvnitř pravidelného pětiúhelníku ABCDE je bod P takový, že trojúhelník ABP je rovnostranný. Jak velký je úhel BCP? Udělej si náčrtek - Pro velikosti
Pro velikosti vnitřních úhlů čtyřúhelníku ABCD platí: úhel alfa je o 26° větší než úhel beta, dvojnásobek úhlu Beta je o 5° menší než úhel gama a úhel gama je o 36° větší než úhel delta. Určete úhly. - Šestiúhelníky
Je čtverec ABCD, čtverec EFGD a obdélnik HIJD, body JG leží na straně CD pričemž platí DJ je menší než DG a body HE leží na straně DA, pričemž platí DH je menší než DE, dále víme že DJ se rovná GC. Šestiúhelník ABCGFE má obvod 96 cm, šestiúhelník EFGJIH m - Čtyřúhelníku 81469
Dán je čtverec ABCD. Střed AB je E, střed BC je F, CD je G a střed DA je H. Spojíme AF, BG, CH a DE. Uvnitř čtverce (přibližně uprostřed) průsečíky těchto úseček vytvoří čtyřúhelník. Vypočítejte obsah tohoto čtyřúhelníku. Děkuji - Trojúhelníky
Dán je čtverec ABCD a na každé jeho straně je zvolených n jejích vnitřních bodů. Určete počet všech trojúhelníků, jejichž vrcholy X, Y, Z leží v těchto bodech a na různých stranách čtverce. - Uhly lich
Je dan lichobeznik ABCD a velikosti vnitřních úhlů. Úhel SDC 32° Úhel SAD 33° Úhel SDA 77° Úhel CBS 29°, kde S je průsečnik uhlopříček. Jaká je velikost úhlu BSA?
