Trojúhelník + lichoběžník
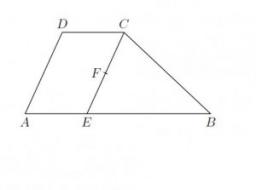
Lichoběžník ABCD se základnami AB=a, CD=c má výšku v. Bod S je střed ramene BC. Dokažte, že obsah trojúhelníku ASD se rovná polovině obsahu lichoběžníku ABCD.
Správná odpověď:
Zobrazuji 1 komentář:
Dr. Math
- Lichoběžník ABCD má základne AB = a , CD = c a výšku v .
- Bod S je střed ramena BC .
Obsah lichoběžníka sa vypočíta podľa vzorca:
Trojúhelník ASD má základňu AD (ktorá je rovnobežná s BC ) a výšku (vzdialenosť bodu S od AD ).
- Rameno BC má dĺžku √(a-c)2 + v2 (ak je lichoběžník všeobecný), ale presná dĺžka nie je pre dôkaz dôležitá.
- Pre súradnicovú analýzu umiestnime lichoběžník do roviny:
- Nech A = (0, 0) , B = (a, 0) , C = (c, v) , D = (0, v) .
- Stred S ramena BC má súradnice:
- Vrcholy trojúhelníka: A(0,0) , S( a+c2, v2 ) , D(0,v) .
- Použijeme determinantový vzorec pre obsah trojúhelníka:
Dosadením súradníc:
Obsah lichoběžníka:
Obsah trojúhelníka ASD :
Obsah trojúhelníka ASD je skutočne polovicou obsahu lichoběžníka ABCD , čo sme mali dokázať. Dôkaz nezávisí od tvaru lichoběžníka, platí pre všetky lichoběžníky s danými základňami a výškou.
- Bod S je střed ramena BC .
Obsah lichoběžníka ABCD
Obsah lichoběžníka sa vypočíta podľa vzorca:
PABCD = a + c2 · v
Obsah trojúhelníka ASD
Trojúhelník ASD má základňu AD (ktorá je rovnobežná s BC ) a výšku (vzdialenosť bodu S od AD ).
a) Poloha bodu S
- Rameno BC má dĺžku √(a-c)2 + v2 (ak je lichoběžník všeobecný), ale presná dĺžka nie je pre dôkaz dôležitá.
- Pre súradnicovú analýzu umiestnime lichoběžník do roviny:
- Nech A = (0, 0) , B = (a, 0) , C = (c, v) , D = (0, v) .
- Stred S ramena BC má súradnice:
S = ( a + c2, 0 + v2 ) = ( a + c2, v2 )
b) Výpočet obsahu Δ ASD
- Vrcholy trojúhelníka: A(0,0) , S( a+c2, v2 ) , D(0,v) .
- Použijeme determinantový vzorec pre obsah trojúhelníka:
PASD = 12 ( x_A(y_S - y_D) + x_S(y_D - y_A) + x_D(y_A - y_S) )
Dosadením súradníc:
PASD = 12 ( 0 ( v2 - v ) + a+c2 (v - 0) + 0 (0 - v2) ) = 12 · (a+c)v2 = (a+c)v4
Porovnanie obsahov
Obsah lichoběžníka:
PABCD = (a + c)2 · v
Obsah trojúhelníka ASD :
PASD = (a + c)v4 = 12 · (a + c)v2 = 12 PABCD
Záver
Obsah trojúhelníka ASD je skutočne polovicou obsahu lichoběžníka ABCD , čo sme mali dokázať. Dôkaz nezávisí od tvaru lichoběžníka, platí pre všetky lichoběžníky s danými základňami a výškou.
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetrietémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Trojúhelníku 3428
Daný je lichoběžník ABCD se základnami AB, CD. Nechť K je střed strany AB a L je střed strany CD. Obsah trojúhelníku ALB je 15 cm² a obsah trojúhelníku DKC je 10 cm². Vypočítejte obsah lichoběžníku ABCD. - Obsah trojúhelníku
Vypočtěte velikost ramene b lichoběžníku ABCD, pokud a = 12 cm, c = 4 cm, d(AC)= d(BC) a obsah S(trojúhelníku ABC) = 9 cm čtverečních. - Čtyřboký hranol 6
Vypočítej povrch čtyřbokého hranolu ABCDA'B'C'D' s lichoběžníkovou podstavou ABCD. Výška hranolu je 12 cm; údaje o lichoběžníku ABCD: délka základny AB je 8 cm, délka základny CD je 3 cm, délka ramene BC je 4 cm a délka úhlopříčky AC je 7 cm. Napovíme: Na - V rovnoramenný lichoběžník
V rovnoramenném lichoběžníku ABCD jsou dány jeho základny AB=20cm, CD=12cm a ramena AD=BC=8cm. Určete jeho výšku a úhel alfa při vrcholu A. - Rovnoramenný 2588
Daný je rovnoramenný lichoběžník ABCD, ve kterém platí |AB|= 2|BC|= 2|CD|= 2|DA|. Na jeho straně BC je bod K takový, že |BK| = 2|KC|, na jeho straně CD je bod L takový, že |CL|= 2|LD|, a na jeho straně DA je bod M takový, že|DM|= 2|MA|. Určete velikosti v - Úhlopříčka deleno tri
V daném obdélníku ABCD je E střed BC a F střed CD. Dokažte, že přímky AE a AF dělí úhlopříčku BD na tři stejné části. - Lichoběžník 21
Je dán lichoběžníku ABCD s rovnoběžnými stranami AB a CD pro bod E strany AB plati, že úsečka DE dělí lichoběžník na dvě části se stejným obsahem. Spočítej délku úsečky AE.
