Důkaz - příklady
Důkaz je v matematice přesvědčivá demonstrace, že nějaké tvrzení je za určitých předpokladů pravdivé.Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.
Počet nalezených příkladů: 42
- Užitím 2
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - Podstavy 82687
Pokud je plášť kužele půlkruh, pak průměr podstavy kužele je stejný jako délka jeho strany. Dokažte. - V trojúhelníku 7
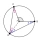V trojúhelníku ABC svírají osy úhlů alpha a beta úhel fí = R + gama/2. R je pravý úhel 90°. Ověřte. - Karel 5
Karel má z pětiminutovek průměr známek přesně 1,12. Dokažte, že z nich má aspoň 22 jedniček. - Polopřímkách 80498
Daný je ostroúhlý trojúhelník ABC. Na polopřímkách opačných k BA a CA leží postupně body D a E tak, že |BD| = |AC| a |CE| = |AB|. Dokažte, že střed kružnice opsané trojúhelníku ADE leží na kružnici opsané trojúhelníku ABC. - Kvadrát a 3. mocnina
Najděte nejmenší x přirozené takové, že 2x je čtverec a 3x je třetí mocnina přirozeného čísla - Nad odvěsnami
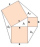Nad odvěsnami a přeponou jsou sestrojeny čtverce. Spojením vnějších vrcholů sousedních čtverců vzniknou tři trojúhelníky. Dokaž, že jejich obsahy jsou stejné.
- Zjednodušte logaritmický výraz
Vzhledem k tomu, že logxU + logxV = p a logxU - logxV =q Dokažte, že U=x^½(p+q) - Pravděpodobnosti 57683
V dílně se k výrobě židlí používají tři roboty Q, R a S Robot Q tvoří 25% židlí Robot R tvoří 45% židlí Zbývající židle vyrobil Robot S Důkazy ukázaly, že 2 procenta židlí vyrobených robotem Q jsou vadné, 3 procenta židlí vyrobených robotem R a 5 procent - Přirozené 55591
Pokud n je přirozené číslo, které dává při dělení 5 zbytek 2 nebo 3, tak n na druhou dává při dělení 5 zbytek 4. Dokažte přímo - Přirozené 55581
Dokažte nepřímo: Žádné liché přirozené číslo není dělitelné čtyřmi. - Standardizovaný
Standardizovaný test byl podán tisícům studentů s průměrným skóre 85 a standardní odchylkou 8. Náhodný vzorek 50 studentů dostal stejný test a ukázal průměrné skóre 83,20. Existují důkazy, které ukazují, že tato skupina má nižší výkon než ty obecně na úro - Posloupnost 36183
Dokažte, že posloupnost { 3 – 4. n } od n=1 po ∞ je klesající. - Bonbony
Miško dostal takový počet bonbonů, že všechny číslice v tomto počtu byly stejné. Dokažte, že vždy pokud umí takový počet bonbonů rozdělit na 72 stejných hromádek, tak je umí rozdělit i na 37 stejných hromádek. (Pozn. : bonbóny neumíme rozlomit) - MO B 2019 ukol 2
Přirozené číslo n má aspoň 73 dvojmístných dělitelů. Dokažte, že jedním z nich je číslo 60. Uveďte rovněž příklad čísla n, které má právě 73 dvojmístných dělitelů, včetně náležitého zdůvodnění.
- Tři operátoři
Tři operátoři vyrobili 480 kusů za 50 minut. Kolik celkem odpracovali hodin? Ve firmě se mi snazi vnutit názor, že je to 2,5 hodiny. Co je tedy správně? Děkuji Petra - C – I – 3 MO 2018
Nechť a, b, c jsou kladná reálná čísla, jejichž součet je 3, a každé z nich je nejvýše 2. Dokažte, že platí nerovnost: a2 + b2 + c2 + 3abc < 9 - Pokračovat 7303
Vyberte si libovolné číslo. Pokud je toto číslo sudé, vydělte ho 2. Pokud je liché, vynásobte ho třemi a přidejte jeden. Nyní zopakujte postup s novým číslem. Pokud budete pokračovat, nakonec vždy skončíte na stejném čísle. dokažte. - Trojúhelníku 7247
Na straně AB trojúhelníku ABC jsou dány body D a E tak, že |AD| = |DE| = |EB|. Body A a B jsou postupně středy úseček CF a CG. Přímka CD protíná přímku FB v bodě I a přímka CE protíná přímku AG v bodě J. Dokažte, že průsečík přímek AI a BJ leží na přímce - Kružnice
Dokažte, že rovnice k1 a k2 představují kružnice. Napište rovnici přímky, která prochází středy těchto kružnic. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0
Máš příklad, nad kterým si přemýšlíš alespoň 10 minut? Pošli nám příklad a my Ti ho zkusíme vypočítat.
