The proof - practice problems
The proof is a convincing demonstration in mathematics that a statement is true under certain conditions.Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 40
- The 5th
The 5th, 8th and 11th terms of a GP are a, b, c respectively. Show that a, b, c are in GP. - And or logic
If A and B are events with P(A)=0.3, P(A OR B)=0.76, and P(A AND B)=0.04, find P(B). Enter your answer in decimal form, rounded to one place. - Prove 2
Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7). - Isosceles triangle and cosine
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
- Semicircle 82687
If the shell of a cone is a semicircle, then the diameter of the cone's base is equal to its side's length. Prove it. - Triangle 80994
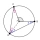In the triangle, ABC, the angles alpha and beta axes subtend the angle phi = R + gamma/2. R is a right angle of 90°. Verify. - Five-minute 80951
Karel has an average grade of exactly 1.12 from five-minute episodes. Prove that at least 22 of them have one. - Janice
Janice said that when you multiply a fraction less than 1 by a nonzero whole number, the product is always less than the whole number. Do you agree? Explain. - Circumscribing 80498
Given is an acute-angled triangle ABC. On the half lines opposite to BA and CA lie successively the points D and E such that |BD| = |AC| and |CE| = |AB|. Prove that the center of the circle circumscribing triangle ADE lies on the circle circumscribing tri
- Smallest 79434
Find the smallest natural x such that 2x is the square and 3x is the third power of a natural number. - Constructed 77874
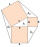Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same. - Bisector 2
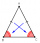ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - Fraction and ratios
Fraction and ratios are different names for the same thing. - Simplify logarithm expr
Given that logxU + logxV =p and logxU - logxV =q Prove that U=x^½(p+q)
- Directly 55591
If n is a natural number that gives a division of 2 or 3 when divided by 5, then n gives a residue of 4 when divided by 5. Prove directly - Indirectly: 55581
Prove indirectly: No odd natural number is divisible by four. - Decreasing 36183
Prove that the sequence {3 - 4. n} from n = 1 to ∞ is decreasing. - Whenever 12151
Mickey got so many candies that all the digits in this number were the same. Prove that whenever he can divide such several candies into 72 equal piles, he can also divide them into 37 equal piles. (Note: candies cannot be broken) - Justification 8468
The natural number n has at least 73 two-digit divisors. Prove that one of them is the number 60. Also, give an example of the number n, which has exactly 73 double-digit divisors, including a proper justification.
Three factory operators produced 480 units in 50 minutes. How many hours worked? I'm trying to prove or disapprove of the idea that the company tells me it's 2.5 hours. So what is right? Thank you, Petra.Do you have unsolved problem that you need help? Ask a question, and we will try to solve it. Solving math problems.
