The proof - practice problems - last page
The proof is a convincing demonstration in mathematics that a statement is true under certain conditions.Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 40
- Inequality 7320
Let a, b, and c be positive real numbers whose sum is 3, each of which is at most 2. Prove that the inequality holds: a2 + b2 + c2 + 3abc - Odd/even number
Pick any number. If that number is even, divide it by 2. If it's odd, multiply it by three and add one. Now, repeat the process with your new number. If you keep going, you'll eventually end up at one every time. Prove. - Intersection 7247
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin - Prove
Prove that k1 and k2 are the equations of two circles. Find the equation of the line that passes through the centers of these circles. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0
- Sum of inner angles
Prove that the sum of all inner angles of any convex n-angle equals (n-2).180 degrees. - Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere. - Trapezoid 4908
Trapezoid ABCD with bases AB = a, CD = c has height v. The point S is the center of the arm BC. Prove that the area of the ASD triangle is equal to half the area of the ABCD trapezoid. - Inequality 4434
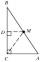The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | holds - Three numbers
How much do we increase the sum of three numbers when the first enlarges by 14, the second by 15, and the third by 16? Choose any three two-digit numbers and prove the results.
- Diagonal in rectangle
In the ABCD rectangle is the center of BC, point E, and point F is the center of the CD. Prove that the lines AE and AF divide diagonal BD into three equal parts. - Theorem prove
We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption do we start? - Truncated cone
Calculate the height of the rotating truncated cone with volume V = 1354 cm³ and a base radii r1 = 9.1 cm and r2 = 5.4 cm. - See harmonics
Is it true that the size of the central segment of any trapezoid is the harmonic mean size of its bases? Prove it. The central segment crosses the intersection of the diagonals and is parallel to the bases. - Laws
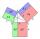From which law directly follows the validity of Pythagoras' theorem in the right triangle? ...
- Proof PT
Can you easily prove Pythagoras' theorem using Euclidean theorems? If so, do it. - Triangle P2
Can a triangle have two right angles? - Triangle
Prove whether you can construct a triangle ABC if a=8 cm, b=6 cm, c=10 cm. - Reciprocal
It is true (prove it) that if a > b > 0: (1)/(a)< (1)/(b) - Proof I
When added to the product of two consecutive integers larger one, we get the square larger one. Is this true or not?
Comical errors, disputes and plots arise when converting physical units. The core of today's dispute was the price of natural gas. The unit was changed - from the natural unit of cubic meter of gas to the unit kWh. The goal was to be able to compare the pDo you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
