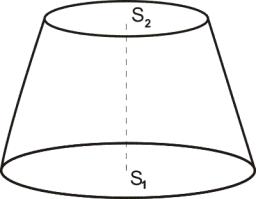
Truncated cone
Calculate the height of the rotating truncated cone with volume V = 1471 cm3 and a base radii r1 = 6.1 cm and r2 = 7.9 cm.
Your answer:
Your answer:
Showing 4 comments:
Kukoslav
need to solve a cubic equation, as obtained above, to find rises in heights... integral
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetryUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Frustrum - volume, area
Calculate the surface and volume of a truncated rotating cone with base radii of 8 cm and 4 cm and a height of 5 cm. - The truncated
The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm, and height v = 5 cm. What is the volume of the cone from which the truncated cone originated? - Cone surface volume
Calculate the surface and volume of the cut rotating cone with base radii of 14 cm and 8 cm height of 11 cm. - Truncated cone
Calculate the volume of a truncated cone with base radiuses r1=19 cm, r2 = 11 cm, and height v = 5 cm. - The surface The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10 cm.
- Top-open tank
The top-open tank resembles a truncated rotating cone, standing on a smaller base. Its volume is 465 m3, and the bases' radii are 4 m and 3 m. Find the tank's depth. - Rotating cone
Calculate the volume of a rotating cone with base radius r=18 cm and height h=20 cm.
