Inequality proof
Let a, b, and c be positive real numbers whose sum is 3, each of which is at most 2.
Prove that the inequality holds:
a2 + b2 + c2 + 3abc <9
Your answer:
Prove that the inequality holds:
a2 + b2 + c2 + 3abc <9
Your answer:
You need to know the following knowledge to solve this word math problem:
algebraarithmeticbasic operations and conceptsthemes, topicsGrade of the word problem
Related math problems and questions:
- Triangle
Prove whether a triangle ABC with the given properties can be constructed: a=8 cm, b=6 cm, c=10 cm. - Inequality triangle
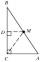The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | < c. - Real and imaginary parts
Let z1=x1+y1i and z2=x2+y2i Find: a = Im (z1z2) b = Re (z1/z2) - ZSE year 2022 comparison
Calculate the limit value of monthly electricity consumption in kWh of rates D1 and D2, at which it is worth it to change the rate (from D1 to D2 or vice versa). The energy company offers the following pricelists (very confusing for an ordinary user, espe - In plane 2
Triangle ABC lies in the plane with a right angle at vertex C, where A(1, 2), B(5, 2), C(x, x+1), and x > −1. a) Determine the value of x. b) Determine the coordinates of point M, the midpoint of segment AB. c) Prove that vectors AB and CM are perpendi - 5 addition problems
No problem; here are five decimal addition problems for you to practice: 1. What is the result of 3.5 + 2.1? 2. What is the result of 0.8 + 0.3? 3. What is the result of 5.2 + 1.7? 4. What is the result of 2.5 + 0.9? 5. What is the result of 1.4 + 0.6? I - Bisector 2
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
