C – I – 3 MO 2018
Nech a, b, c sú kladné reálne čísla, ktorých súčet je 3, a každé z nich je nanajvýš 2.
Dokážte, že platí nerovnosť:
a2 + b2 + c2 + 3abc < 9
Dokážte, že platí nerovnosť:
a2 + b2 + c2 + 3abc < 9
Správna odpoveď:
Zobrazujem 4 komentáre:
Dr Math
to je limittny pripad; a=b=c=2 pren plati ze lava strana sa rovna pravej. Pre pripady a+b+c=3 je to L>P
6 rokov 1 Like
Dr Math
Návodné úlohy ( to sme nevymysleli my, ale asi autor prikladu):
N1. Pre reálne čísla so súčtom 3 platí navyše a2 + b2 + c2 = 5. Aké hodnoty môže nadobúdať výraz ab + bc + ca? [Keďže (a + b + c)2 = a2 + b2 + c2 + 2 (ab + bc + ca), je nutne ab + bc + ca = 2. Hodnota je dosiahnuteľná vďaka trojici (2 , 1, 0).]
N2. Nezáporné reálne čísla a, b, c sú všetky neprekračovať 1. Dokážte, že 3abc <= a + b + c. Kedy nastane rovnosť? [Upravíme na a (1 - bc) + b (1 - ac) + c (1 - ab)> = 0, výrazy v zátvorkách sú nezáporné. Rovnosť nastane práve keď buď a = b = c = 0, alebo a = b = c = 1.]
D1. Dokážte, že pre reálne čísla a, b, c platí a2 + b2 + c2> = ab + bc + ca. Kedy nastane rovnosť? [Nerovnosť je ekvivalentná s (a - b)2 + (b - c)2 + (c - a)2 = 0, ktorá iste platí. Rovnosť nastane jedine v prípade a = b = c.]
D2. Reálne čísla a, b, c majú súčet 3. Dokážte, že 3 = ab + bc + ca. Kedy nastane rovnosť? [Plynie z rovnosti 9 = (a + b + c)2 = a2 + b2 + c2 + 2 (ab + bc + ca) a z predošlej úlohy. Rovnosť nastane jedine v prípade a = b = c = 1.]
D3. Dokážte, že pre ľubovoľné reálne čísla x, y, z platí nerovnosť x2 + 5y2 + 4z2 = 4y (x + z), a zistite, kedy nastane rovnosť. [Anulujte pravú stranu danej nerovnosti a upravte ju následne do tvaru (x2 - 4xy + 4y2) + (y2 - 4yz + 4z2) = 0, kde na ľavej strane je nezáporný súčet (x - 2y)2 + (y - 2z)2. Rovnosť tu nastane práve vtedy, keď platí (x, y, z) = (4c, 2c, c), kde c je ľubovoľné reálne číslo.]
D4. Nech a, b, c sú dĺžky strán trojuholníka. Dokážte, že platí nerovnosť 3a2 + 2BC> 2ab + 2AC. [Danú nerovnosť upravte na tvar a 2 - (b-c)2 + (a-b)2 + (a-c)2> 0 a rozdiel prvých dvoch druhých mocnín nahraďte príslušným súčinom.]
N1. Pre reálne čísla so súčtom 3 platí navyše a2 + b2 + c2 = 5. Aké hodnoty môže nadobúdať výraz ab + bc + ca? [Keďže (a + b + c)2 = a2 + b2 + c2 + 2 (ab + bc + ca), je nutne ab + bc + ca = 2. Hodnota je dosiahnuteľná vďaka trojici (2 , 1, 0).]
N2. Nezáporné reálne čísla a, b, c sú všetky neprekračovať 1. Dokážte, že 3abc <= a + b + c. Kedy nastane rovnosť? [Upravíme na a (1 - bc) + b (1 - ac) + c (1 - ab)> = 0, výrazy v zátvorkách sú nezáporné. Rovnosť nastane práve keď buď a = b = c = 0, alebo a = b = c = 1.]
D1. Dokážte, že pre reálne čísla a, b, c platí a2 + b2 + c2> = ab + bc + ca. Kedy nastane rovnosť? [Nerovnosť je ekvivalentná s (a - b)2 + (b - c)2 + (c - a)2 = 0, ktorá iste platí. Rovnosť nastane jedine v prípade a = b = c.]
D2. Reálne čísla a, b, c majú súčet 3. Dokážte, že 3 = ab + bc + ca. Kedy nastane rovnosť? [Plynie z rovnosti 9 = (a + b + c)2 = a2 + b2 + c2 + 2 (ab + bc + ca) a z predošlej úlohy. Rovnosť nastane jedine v prípade a = b = c = 1.]
D3. Dokážte, že pre ľubovoľné reálne čísla x, y, z platí nerovnosť x2 + 5y2 + 4z2 = 4y (x + z), a zistite, kedy nastane rovnosť. [Anulujte pravú stranu danej nerovnosti a upravte ju následne do tvaru (x2 - 4xy + 4y2) + (y2 - 4yz + 4z2) = 0, kde na ľavej strane je nezáporný súčet (x - 2y)2 + (y - 2z)2. Rovnosť tu nastane práve vtedy, keď platí (x, y, z) = (4c, 2c, c), kde c je ľubovoľné reálne číslo.]
D4. Nech a, b, c sú dĺžky strán trojuholníka. Dokážte, že platí nerovnosť 3a2 + 2BC> 2ab + 2AC. [Danú nerovnosť upravte na tvar a 2 - (b-c)2 + (a-b)2 + (a-c)2> 0 a rozdiel prvých dvoch druhých mocnín nahraďte príslušným súčinom.]
6 rokov 1 Like
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Súvisiace a podobné príklady:
- Dôkaz - MO - C – I – 3
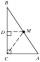Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1:2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť 3|a-b| < c. - Trojuholníka 81613
V rovine je umiestnený trojuholník ABC s pravým uhlom pri vrchole C, pre ktorý platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určite hodnotu x b) určite súradnice bodu M, ktorý je stredom úsečky AB c) dokážte že vektory AB a CM sú kolmé d) určite v - Rovnoramenný 3uholník dôkaz
Použitím kosínovej vety dokážte, že v rovnoramennom trojuholníku ABC so základňou AB platí, že c=2a cos α. - Komplexné
Sú tieto čísla 2i, 4i, 1+2i, 8i, 3+2i, 4+7i, 8i, 8i+4, 5i, 6i, 3i komplexné?
- Aký je 3
Aký je súčet všetkých súradníc bodov, ktoré sú priesečníkmi priamky p: x = -1-2t, y = 5-4t, z = -3+6t, kde t je reálne číslo, so súradnicovými rovinami xy a yz? - Dve čísla
Dve čísla sú v pomere 3:2. Ak by sme každé z nich zväčšili o 5, boli by v pomere 4:3. Aký je súčet pôvodných čísel? - Trojuhoľníky 4
Trojuhoľníky ABC a A'B'C' sú podobné. V trojuhoľníku ABC sú veľkosti dvoch uhlov 25° a 65°. Zdôvodni, prečo v trojuhoľníku A'B'C' je súčet veľkostí dvoch uhlov rovný 90°.
