Dôkaz - MO - C – I – 3
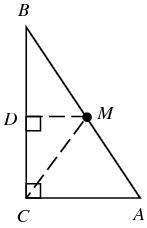
Päta výšky z vrcholu C v trojuholníku ABC delí stranu AB v pomere 1:2. Dokážte, že pri zvyčajnom označení dĺžok strán trojuholníka ABC platí nerovnosť 3∣a−b∣<c.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
Téma:
Úroveň náročnosti úlohy:
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Štvorce
Na dvoma stranami trojuholníka ABC sú zostrojené štvorce. Obsah štvorca nad stranou BC je 25 cm². Veľkosť výšky vc na stranu AB je 3 cm. Pata P výšky vc delí stranu AB v pomere 2:1. Strana AC je dlhšia ako strana BC. Vypočítajte v cm dĺžku strany AB. Vypo - Kosodĺžnik 5
Určte obvod a obsah kosodĺžnika ABCD, ktorého kratšia strana AD má dĺžku 5 cm a päta výšky vedené vrcholom D k strane AB delí stranu AB na dva úseky dĺžok 3 cm a 4 cm. - Trojuholník ABC
V trojuholníku ABC so stranou BC dĺžky 2 cm je bod K stredom strany AB. Body L a M rozdeľujú stranu AC na tri zhodné úsečky. Trojuholník KLM je rovnoramenný s pravým uhlom pri vrchole K. Určte dĺžky strán AB, AC trojuholníka ABC. - Rovnoramennom 83157
Použitím kosínovej vety dokážte, že v rovnoramennom trojuholníku ABC so základňou AB platí, že c=2a cos α.
- V pravouhlom 12
V pravouhlom trojuholníku má prepona dĺžku 24cm. Päta výšky na preponu ju delí na dve časti v pomere 2:4. Akú veľkosť v cm má výška na preponu? Vypočítajte v centimetroch obvod tohto pravouhlého trojuholníka. - Trojuholníka 81019
V pravouhlom trojuholníku ABC (AB je prepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítajte dĺžky strán trojuholníka ABC. - C – I – 3 MO 2018
Nech a, b, c sú kladné reálne čísla, ktorých súčet je 3, a každé z nich je nanajvýš 2. Dokážte, že platí nerovnosť: a2 + b2 + c2 + 3abc < 9
