C – I – 3 MO 2018
Nechť a, b, c jsou kladná reálná čísla, jejichž součet je 3, a každé z nich je nejvýše 2.
Dokažte, že platí nerovnost:
a2 + b2 + c2 + 3abc < 9
Dokažte, že platí nerovnost:
a2 + b2 + c2 + 3abc < 9
Správná odpověď:

Zobrazuji 3 komentáře:
Dr Math
Návodné a doplňující úlohy:
N1. Pro reálná čísla se součtem 3 platí navíc a2 + b2 + c2 = 5. Jaké hodnoty může nabývat výraz ab+bc+ca? [Jelikož (a+b+c)2 = a2 +b2 +c2 + 2(ab+bc+ca), je nutně ab + bc + ca = 2. Hodnota je dosažitelná díky trojici (2, 1, 0).]
N2. Nezáporná reálná čísla a, b, c jsou všechna nejvýše rovna 1. Dokažte, že 3abc <= a + b + c. Kdy nastane rovnost? [Upravíme na a(1 − bc) + b(1 − ac) + c(1 − ab) >= 0, výrazy v závorkách jsou nezáporné. Rovnost nastane, právě když buď a = b = c = 0, nebo a = b = c = 1.]
D1. Dokažte, že pro reálná čísla a, b, c platí a2 +b2 +c2 >= ab+bc+ca. Kdy nastane rovnost? [Nerovnost je ekvivalentní s (a − b)2 + (b − c)2 + (c − a)2 = 0, která jistě platí. Rovnost nastane jedině v případě a = b = c.]
D2. Reálná čísla a, b, c mají součet 3. Dokažte, že 3 = ab + bc + ca. Kdy nastane rovnost? [Plyne z rovnosti 9 = (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca) a z předešlé úlohy. Rovnost nastane jedině v případě a = b = c = 1.]
D3. Dokažte, že pro libovolná reálná čísla x, y, z platí nerovnost x2 + 5y2 + 4z2 = 4y(x + z), a zjistěte, kdy nastane rovnost. [Anulujte pravou stranu dané nerovnosti a upravte ji následně do tvaru (x2 − 4xy + 4y2 ) + (y2 − 4yz + 4z2 ) = 0, kde na levé straně je nezáporný součet (x − 2y)2 + (y − 2z)2 . Rovnost zde nastane, právě když platí (x, y, z) = (4c, 2c, c), kde c je libovolné reálné číslo.]
D4. Nechť a, b, c jsou délky stran trojúhelníku. Dokažte, že platí nerovnost 3a2 + 2bc > 2ab + 2ac. [Danou nerovnost upravte na tvar a 2 −(b−c)2 + (a−b)2 + (a−c)2 > 0 a rozdíl prvních dvou druhých mocnin nahraďte příslušným součinem.]
N1. Pro reálná čísla se součtem 3 platí navíc a2 + b2 + c2 = 5. Jaké hodnoty může nabývat výraz ab+bc+ca? [Jelikož (a+b+c)2 = a2 +b2 +c2 + 2(ab+bc+ca), je nutně ab + bc + ca = 2. Hodnota je dosažitelná díky trojici (2, 1, 0).]
N2. Nezáporná reálná čísla a, b, c jsou všechna nejvýše rovna 1. Dokažte, že 3abc <= a + b + c. Kdy nastane rovnost? [Upravíme na a(1 − bc) + b(1 − ac) + c(1 − ab) >= 0, výrazy v závorkách jsou nezáporné. Rovnost nastane, právě když buď a = b = c = 0, nebo a = b = c = 1.]
D1. Dokažte, že pro reálná čísla a, b, c platí a2 +b2 +c2 >= ab+bc+ca. Kdy nastane rovnost? [Nerovnost je ekvivalentní s (a − b)2 + (b − c)2 + (c − a)2 = 0, která jistě platí. Rovnost nastane jedině v případě a = b = c.]
D2. Reálná čísla a, b, c mají součet 3. Dokažte, že 3 = ab + bc + ca. Kdy nastane rovnost? [Plyne z rovnosti 9 = (a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca) a z předešlé úlohy. Rovnost nastane jedině v případě a = b = c = 1.]
D3. Dokažte, že pro libovolná reálná čísla x, y, z platí nerovnost x2 + 5y2 + 4z2 = 4y(x + z), a zjistěte, kdy nastane rovnost. [Anulujte pravou stranu dané nerovnosti a upravte ji následně do tvaru (x2 − 4xy + 4y2 ) + (y2 − 4yz + 4z2 ) = 0, kde na levé straně je nezáporný součet (x − 2y)2 + (y − 2z)2 . Rovnost zde nastane, právě když platí (x, y, z) = (4c, 2c, c), kde c je libovolné reálné číslo.]
D4. Nechť a, b, c jsou délky stran trojúhelníku. Dokažte, že platí nerovnost 3a2 + 2bc > 2ab + 2ac. [Danou nerovnost upravte na tvar a 2 −(b−c)2 + (a−b)2 + (a−c)2 > 0 a rozdíl prvních dvou druhých mocnin nahraďte příslušným součinem.]
Žák
A co tohle jestli a, b, c jsou kladná reálná čísla a ab + bc + ca = 1 najděte hodnotu tohoto výrazu (b2+1) /a+b + b (c2+1) /b+c + c (a2+1) /c+a?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikazákladní operace a pojmytémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Výška v trojúhelníku
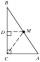 Pata výšky z vrcholu C v trojúhelníku ABC dělí stranu AB v poměru 1:2. Dokažte, že při obvyklém označení délek stran trojúhelníku ABC platí nerovnost 3|a-b| < c.
Pata výšky z vrcholu C v trojúhelníku ABC dělí stranu AB v poměru 1:2. Dokažte, že při obvyklém označení délek stran trojúhelníku ABC platí nerovnost 3|a-b| < c. - Dvě čísla
 Znám dvě čísla, jejichž součet 20. Když ale každé z nich zaokrouhlím na desítky a pak sečtu, dostanu 30.
Znám dvě čísla, jejichž součet 20. Když ale každé z nich zaokrouhlím na desítky a pak sečtu, dostanu 30. - Užitím 2
 Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α.
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - V rovině 2
 V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel - Rozdíl mezi X a Y
 X a Y jsou kladná celá čísla. Pokud X+Y+XY=32, jaký je rozdíl mezi X a Y?
X a Y jsou kladná celá čísla. Pokud X+Y+XY=32, jaký je rozdíl mezi X a Y? - Student
 Student má udělat test, který obsahuje 10 otázek. U každé z nich vybírá jednu z 5 odpovědí, přičemž právě jedna je správná. Student se na test nepřipravil, a proto odpovědi volí náhodně. Jaké jsou pravděpodobnosti, že student zodpoví správně: a) nejvýše 3
Student má udělat test, který obsahuje 10 otázek. U každé z nich vybírá jednu z 5 odpovědí, přičemž právě jedna je správná. Student se na test nepřipravil, a proto odpovědi volí náhodně. Jaké jsou pravděpodobnosti, že student zodpoví správně: a) nejvýše 3 - Přímka
 Daná je přímka, která prochází body A [-3; 22] a B [33; -2]. Určete počet všech bodů této přímky, jejichž obě souřadnice jsou kladná celá čísla.
Daná je přímka, která prochází body A [-3; 22] a B [33; -2]. Určete počet všech bodů této přímky, jejichž obě souřadnice jsou kladná celá čísla.
