Decreasing 36183
Prove that the sequence {3 - 4. n} from n = 1 to ∞ is decreasing.
Result
Result
You need to know the following knowledge to solve this word math problem:
algebraarithmeticnumbersthemes, topicsGrade of the word problem
Related math problems and questions:
- Five members
Write the first five members of the geometric sequence and determine whether it is increasing or decreasing: a1 = 3 q = -2 - Geometric progression 4
There is a number sequence: 8,4,√2,4,2√2 Prove that the sequence is geometric. Find the common ratio and the following three members. - Bisector 2
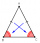ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - Inequality 4434
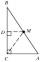The heel of height from the vertex C in the triangle ABC divides the side AB in the ratio 1:2. Prove that in the usual notation of the lengths of the sides of the triangle ABC, the inequality 3 | a-b | holds
- Simplify logarithm expr
Given that logxU + logxV =p and logxU - logxV =q Prove that U=x^½(p+q) - Prove
Prove that k1 and k2 are the equations of two circles. Find the equation of the line that passes through the centers of these circles. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0 - Isosceles triangle and cosine
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
