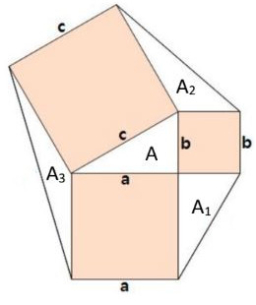
Constructed 77874
Squares are constructed above the overhangs and the transom. Connecting the outer vertices of adjacent squares creates three triangles. Prove that their areas are the same.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Constructed triangle
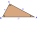 The perimeter of the right triangle is 18 cm. The sum of the areas of the squares constructed above its three sides is 128 cm². What is the area of the triangle?
The perimeter of the right triangle is 18 cm. The sum of the areas of the squares constructed above its three sides is 128 cm². What is the area of the triangle? - Combi-triangle
 Each square side is marked 13 different points outside the square's vertices. How many triangles can be constructed from this set of points, where each vertex of the triangle lies on the other side of the square?
Each square side is marked 13 different points outside the square's vertices. How many triangles can be constructed from this set of points, where each vertex of the triangle lies on the other side of the square? - Infinite sum of areas
 An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Squares above sides
 In a right triangle, the areas of the squares above its sides are 169, 25, and 144. The length of its longer leg is:
In a right triangle, the areas of the squares above its sides are 169, 25, and 144. The length of its longer leg is: - Internal angles
 The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Squares above sides
 Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2:1 ratio. The AC side is longer than the BC side. Calcu
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2:1 ratio. The AC side is longer than the BC side. Calcu - Perimeters 81399
 Two squares are given. The first has a side length of 5 cm, the second 10 cm. Write the ratio of: for a- of their sides for b- their perimeters for c- their areas
Two squares are given. The first has a side length of 5 cm, the second 10 cm. Write the ratio of: for a- of their sides for b- their perimeters for c- their areas
