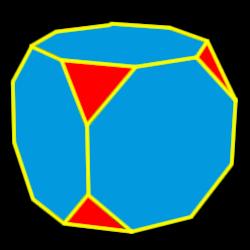
Cube corners
All vertices are cut off a cube with edge 24 cm such that each cutting plane intersects the edges 2 cm from the nearest vertex.
How many edges does the resulting solid have?
How many edges does the resulting solid have?
Final Answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
solid geometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Cube diagonals
Cube edge length 5cm. Draw different diagonals. - Isosceles weight
A designer weight is made from a glass cube by cutting a three-sided prism with an isosceles triangle base that is right-angled and whose arm is half the length of the cube edge. What percentage of the cube is cut off when making the weight? - Cube corners
We cut a small cube with an edge length of 2 cm from each corner of a large cube with an edge length of 10 cm. How many cm³ was the body left from the big cube after cutting the small cubes? - Sphere cut
A sphere segment is cut off from a sphere k with radius r = 1. The volume of the sphere inscribed in this segment is equal to 1/6 of the segment's volume. What is the distance of the cutting plane from the center of the sphere? - Shortest walk
An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point - Cutting the prism
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - Cube edge volume
The sum of the lengths of all the cube's edges is 60 cm. How to calculate its volume?
