Isosceles - isosceles
It is given a triangle ABC with sides /AB/ = 3 cm /BC/ = 10 cm, and the angle ABC = 120°. Draw all points X such that the BCX triangle is an isosceles and triangle ABX is an isosceles with the base AB.
Final Answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Conditions 7186
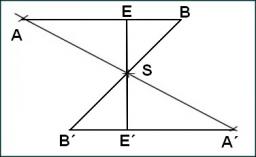
 Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point
Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Draw triangle
 Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm.
Construct an isosceles triangle ABC, if AB = 7cm, the size of the angle ABC is 47°, arms | AC | = | BC |. Measure the size of the BC side in mm. - Triangle ABC
 There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - Rhombus construct
 Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm.
Construct parallelogram (rhombus) ABCD, | AB | = 4 cm alpha = 30° and | BD | = 5 cm. - Bisector 2
 ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC.
ABC is an isosceles triangle. While AB=AC, AX is the bisector of the angle ∢BAC meeting side BC at X. Prove that X is the midpoint of BC. - Main/central vertex
 ABC is an isosceles triangle with base BC and central vertex A. The angle at vertex A is 18°. What will be the size of the angle at vertex B?
ABC is an isosceles triangle with base BC and central vertex A. The angle at vertex A is 18°. What will be the size of the angle at vertex B? - Coefficient 6672
 In the triangle ABC is [AB] = 20cm, [BC] = 10cm, A = 30 °. Construct a triangle A'B'C' similar to triangle ABC if the similarity coefficient is 0.5
In the triangle ABC is [AB] = 20cm, [BC] = 10cm, A = 30 °. Construct a triangle A'B'C' similar to triangle ABC if the similarity coefficient is 0.5
