Laws
Tips for related online calculators
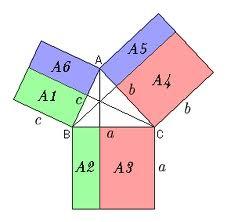
The Pythagorean theorem is the base for the right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsUnits of physical quantitiesthemes, topicsGrade of the word problem
Related math problems and questions:
- Short cut
Imagine that you are going to a friend. That path has a length of 120 meter. Then turn doprava and go other 630 meters, and you are at a friend's. The question is, how much will the journey be shorter if you go directly across the field? - Three vertices
The vertices of triangle ABC are: A[1, 2, -3], B[0, 1, 2], C[2, 1, 1]. Calculate the lengths of sides AB, AC and the angle at vertex A. - Isosceles trapezoid 3
In the isosceles trapezoid ABCD, calculate the unknown side length "a" and its area. Side b = d = 50 cm, c = 20 cm, height = 48 cm. - Triangle 90
Triangle made by 6 cm 4.5 cm and 7.5 cm. what angles does it make? - Triangle
Plane coordinates of vertices: K[9, 5] L[-4, 8] M[3, 20] give Triangle KLM. Calculate its area and its interior angles. - Observation angle
At what angle of view does an object 70 m long appear to the observer, 50 m away from one end and 80 m from the other end? - Triangle Euclid parameters
Using Euclid's Theorems and Pythagoras' Theorem, complete the following parameters describing a right-angled triangle ABC with a right angle at vertex C if we know b=10, cb=8
