MO8-Z8-I-5 2017
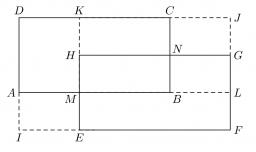
Identical rectangles ABCD and EFGH are positioned such that their sides are parallel to the same. The points I, J, K, L, M, and N are the intersections of the extended sides, as shown. The area of the BNHM rectangle is 12 cm2, the rectangle MBCK area is 63 cm2, and the rectangle MLGH area is 28 cm2. Find the area of the IFJD rectangle.
Correct answer:
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Roland 2
 Roland sold his watch at 15% loss. If he had sold it for 210 USD more, he would have made a profit of 20%. Find the cost of price of the watch.
Roland sold his watch at 15% loss. If he had sold it for 210 USD more, he would have made a profit of 20%. Find the cost of price of the watch. - Remainder one
 Find the least number, when divided by 2,3,4,5,6 and 7 leaves remainder 1 in each case.
Find the least number, when divided by 2,3,4,5,6 and 7 leaves remainder 1 in each case. - Divisible by three
 What least value must be assigned to the blank space so that the number 789563 is divisible by 3
What least value must be assigned to the blank space so that the number 789563 is divisible by 3 - Use the formula for area
 A parallelogram has sides of 15 cm and 12 cm. If the distance between 15 cm sides is 6 cm, find the distance between 12 cm sides.
A parallelogram has sides of 15 cm and 12 cm. If the distance between 15 cm sides is 6 cm, find the distance between 12 cm sides.
- Father and son 10
 Two years ago, Philip was 3 times as old as his son, and 2 years hence, twice his age will be equal to 5 times that of his son. Find their present ages.
Two years ago, Philip was 3 times as old as his son, and 2 years hence, twice his age will be equal to 5 times that of his son. Find their present ages. - Two places 3
 The distance between two places A and B 90 km. Two cars start together from A and B .If both the cars go in the same direction, they meet after 9 hours and if they go in opposite directions they meet after 9/7 hours . Find their speeds .(Assume that A has
The distance between two places A and B 90 km. Two cars start together from A and B .If both the cars go in the same direction, they meet after 9 hours and if they go in opposite directions they meet after 9/7 hours . Find their speeds .(Assume that A has - Students
 In a school 2/5 of total numbers of students comes by car while 1/4 by bus, and others walks to school, of which 1/3 walks on their own and rest are escorted by their parents. If 224 students comes to school walking on their own. Find the total number of
In a school 2/5 of total numbers of students comes by car while 1/4 by bus, and others walks to school, of which 1/3 walks on their own and rest are escorted by their parents. If 224 students comes to school walking on their own. Find the total number of - An adventurer
 An adventurer makes 2/5 of a car trip, 1/3 on horseback and the rest on foot he walks 80 km. What is the total length of your route?
An adventurer makes 2/5 of a car trip, 1/3 on horseback and the rest on foot he walks 80 km. What is the total length of your route? - The test 3
 The provided test marks for a small class of student are as follows Don 70%, Jody 68%, Raz 65% and that of Max is not provided. If the class average is 75%, what is Max test marks?
The provided test marks for a small class of student are as follows Don 70%, Jody 68%, Raz 65% and that of Max is not provided. If the class average is 75%, what is Max test marks?
- Two persons
 Two persons are walking beside a railway track at respective speeds of 2 and 4 km per hour in the same direction. A train came from behind them and crossed them in 90 and 100 seconds, respectively. Find the length of the train.
Two persons are walking beside a railway track at respective speeds of 2 and 4 km per hour in the same direction. A train came from behind them and crossed them in 90 and 100 seconds, respectively. Find the length of the train. - 20 men
 20 men are supposed to complete a work in 10 days. After working for 5 days, they realize that only one-fourth of the work is done. How many more men they need to employ to complete the work on time?
20 men are supposed to complete a work in 10 days. After working for 5 days, they realize that only one-fourth of the work is done. How many more men they need to employ to complete the work on time? - Offset the mean
 The mean of 16 numbers is 8. If 2 is added to every number, what will be the new mean?
The mean of 16 numbers is 8. If 2 is added to every number, what will be the new mean? - Paul makes
 Paul makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube?
Paul makes a cuboid of plasticine of sides 5 cm, 2 cm, 5 cm. How many such cuboids will he need to form a cube? - To percentages
 Convert the following ratios to percentages. (a) 3 : 4 (b) 2 : 3 (c) 5/8 (d) 15/16
Convert the following ratios to percentages. (a) 3 : 4 (b) 2 : 3 (c) 5/8 (d) 15/16
- Overtime and salary
 An employee earns R150 per hour, and the agreed normal working hours are 45 hours per week. Overtime is paid at 1 1/2 of the normal rate. Suppose Dave works 52 hrs during the first week of March. What will the total earnings for that particular week be?
An employee earns R150 per hour, and the agreed normal working hours are 45 hours per week. Overtime is paid at 1 1/2 of the normal rate. Suppose Dave works 52 hrs during the first week of March. What will the total earnings for that particular week be? - Double sides
 If each side of a triangle is doubled, then find the ratio of the area of the new triangle thus formed to the given triangle.
If each side of a triangle is doubled, then find the ratio of the area of the new triangle thus formed to the given triangle. - Taps and a tank
 A tap can fill a tank in 6 hours. After half the tank is filled, three more similar taps are opened. What is the total time taken to fill the tank completely?
A tap can fill a tank in 6 hours. After half the tank is filled, three more similar taps are opened. What is the total time taken to fill the tank completely?
