Maple
The maple peak is visible from a distance of 7 m from the trunk from a height of 1.8 m at an angle of 46°. Find the height of the maple.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
planimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- View angle
At a distance of 10 m from the river bank, they measured the base AB = 50 m parallel to the bank. Point C on the other bank of the river is visible from point A at an angle of 32°30' and from point B at an angle of 42°15'. Calculate the width of the river - TV tower
Calculate the height of the television tower if an observer standing 430 m from the base of the tower sees the peak at an altitude angle of 23°. - Broken tree
The tree is broken at 4 meters above the ground. The top of the tree touches the ground at a distance of 5 meters from the trunk. Calculate the original height of the tree. - Power line pole
From point A, the power pole is visible at an angle of 18 degrees. From place B, which we reach if we go from place A 30m towards the pillar at an angle of 10 degrees. Find the height of the power pole. - A radio antenna
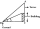Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Determine 8133
Determine the distance between two places, M, and N, between which there is an obstacle so that place N is not visible from place M. The angles MAN = 130°, NBM = 109°, and the distances |AM| = 54, |BM| = 60, while the points A, B, and M lie on one straigh - Mast
The mast has 16 a long shadow on a slope rising from the mast foot in the direction of the shadow angle at angle 9.7°. Determine the height of the mast if the sun above the horizon is at an angle 40°48'.
