Isolating a variable in the formula - math word problems - page 18 of 145
Number of problems found: 2890
- Calculate 83068
The internal volume of the barrel is 15 times greater than the bucket's volume. The volume of the bucket is 5 times the volume of the kettle. We took a third of the water from a barrel, leaving 60 liters in it. Calculate the volume of the kettle in liters - Function: 83053
The inverse function to the function f(x) = √(x-3) for x ≥ 3 is the function: - Completely 83045
The diesel tank has a volume of 19.6 hl. The inflow oven, which flows 17.5 l per minute, was opened for 1.5 hours. How long does the inlet pipe need to be opened for the tank to be completely filled? - Interpretation 83015
A cargo boat with a total weight of 4,500t sailed from the river to the sea. Calculate by how many tons it is possible to increase the weight of the cargo on the boat at sea so that the draft remains the same as in the river. The density of river water is - Arithmetically 83012
There were 21 pupils in the class, and arithmetically, the average height of these pupils was 163 cm. Calculate what the average height in the class will be if: a) A 159 cm tall student was added to the class b) A 169 cm tall student left the class - Seedlings 82997
If you plant seedlings in the bed at a distance of 20 cm, 40 will fit here. How many seedlings will fit here if you reduce the distance between them to 15 cm? - Centimeters - trapezoid
The area of the trapezoid is 132 cm². The difference in the length of both bases is 6 cm, and the height is 2 cm longer than the shorter base. Find the height of the trapezoid in centimeters. - Perpendicular 82994
The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis. - Calculate cuboid
Given cuboid ABCDEFGH. We know that |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Calculate in degrees the angle size formed by the lines BG and FH . - Cylinder express radius
Please express r from the formula for the surface of the cylinder. - Family in ratio
The ages of the father, mother, daughter, and son are in the ratio 11:9:3:2. The mom is 36 years old. What is the sum of their ages? - Simultaneously 82966 The tank with a volume of 15 hl has two inlets. One flows 5 liters per minute, the other 3 liters per minute. How long will it take for the tank to be filled with both inflows simultaneously?
- Concerning 82883
Conductor A has an electrical potential of +140V concerning the Earth; conductor B has a potential of -60V. How much electric charge will we transfer from wire B to wire A if we do the work of 4.10-4 Joules? - Dominika 82882
Dominika and Ninka are in the park. A 48 kg girl sits on the right side of the swing at a distance of 1.9 m from the axis of rotation. Dominika acts on the swing on the left side with a specific force at 2 m from the axis. What force should she exert to k - Diagonals 82850
How do I find the diagonals of a rhombus if its perimeter is 80dm and one diagonal is 2x larger than the other? - Iron ball
Calculate the radius of an iron ball with a density of 7.8g/cm³ and a mass of 7kg. - Rectangular 82803
A rectangular flower bed, one side formed by a wall, must be fenced off with 8-meter-long mesh. What should the flower bed length be so the area is as large as possible? - Quadrilateral pyramid
Construct a 3D model of a quadrilateral pyramid with a rectangle base and sides of isosceles triangles, with a volume of 80 cubic cm. I need to know the sides and the height. - Rectangle 82740
A square in a grid contains 36 squares. This is one-fifth of the number of squares of a rectangle whose side is 30 squares long. What is the length of the other side of the rectangle? Thank you - Determine 82724
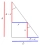A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the area of this square.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
