Practice problems of the volume - page 22 of 118
Volume is the measure of the space that a body fills or occupies. The basic SI unit of volume is the cubic meter. It is the volume of a cube with an edge of one meter, i.e., 1 m x 1 m x 1 m. Significant another unit is 1 l (one liter), 1 m3 = 1000 l applies. One hectoliter (1 hl) is 100 liters.Volume is always the third power of length. Or volume = area times length. For example, the volume of the cube is a3, and the prism's volume is S*h (the area of the base times the height). The volume of rotating bodies (sphere, cone) can be derived in high school by integration. The pyramid's volume is always 1/3 of the prism's volume. We calculate the volume of the truncated bodies either with a formula or simply by subtracting the volumes of the two bodies.
Number of problems found: 2353
- Kilograms 66864
 The sculptor composes an ice city from ice cubes. The cube with an edge length of 2 dm weighs 7.2 kg. How many kilograms is an ice cube with an edge length of 6 dm heavier than it?
The sculptor composes an ice city from ice cubes. The cube with an edge length of 2 dm weighs 7.2 kg. How many kilograms is an ice cube with an edge length of 6 dm heavier than it? - Milliliters 66834
 The cube-shaped vase contains 320 ml of water, which reaches a height of 5 CM. How many milliliters of water can we pour into the vase, so the water does not run out?
The cube-shaped vase contains 320 ml of water, which reaches a height of 5 CM. How many milliliters of water can we pour into the vase, so the water does not run out? - Cylindrical 66744
 How many liters will fit in a cylindrical container with a base area of 0.06 m² and a height of 5 cm?
How many liters will fit in a cylindrical container with a base area of 0.06 m² and a height of 5 cm? - Measuring 66734
 How many 8-liter cans can we fill from a block tank measuring 1.2 * 1m * 1.6m?
How many 8-liter cans can we fill from a block tank measuring 1.2 * 1m * 1.6m?
- Percentage 66684
 Prism with square base a=25cm, height h=45cm. cube: b=15cm a) what percentage of the volume of the prism is the volume of the cube? b) what height should the prism have to have the same volume as the cube?
Prism with square base a=25cm, height h=45cm. cube: b=15cm a) what percentage of the volume of the prism is the volume of the cube? b) what height should the prism have to have the same volume as the cube? - Hexagonal 66574
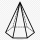 The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax.
The candle is made from wax in the shape of a regular hexagonal pyramid. It has a height of 6.5 cm and a length of the base edge of 3 cm. Find the volume of wax. - Right-angled 66364
 From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area.
From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area. - Difference 66354
 A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle.
A circle is inscribed in a square with a side of 12 cm so that it touches all its sides. Calculate the difference between the area of the square and the circle. - Right-angled 66344
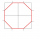 From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm².
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm².
- Deciliters 66324
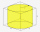 We placed the largest possible lead cylinder in a 1-liter cube container. How many deciliters of water will now fit in the container?
We placed the largest possible lead cylinder in a 1-liter cube container. How many deciliters of water will now fit in the container? - Quadrilateral 66294
 Calculate the surface and volume of a quadrilateral prism if given: the area of the base is 40 cm square, the bottom of the base is k = 8 cm, and the height of the prism is 1.3 dm (the bottom is a rectangle)
Calculate the surface and volume of a quadrilateral prism if given: the area of the base is 40 cm square, the bottom of the base is k = 8 cm, and the height of the prism is 1.3 dm (the bottom is a rectangle) - Enlarge 66284
 We will enlarge the line 8 cm long in the ratio of 7:4. How long in cm will the new line be?
We will enlarge the line 8 cm long in the ratio of 7:4. How long in cm will the new line be? - Perpendiculars 66274
 The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle?
The perpendiculars of a right triangle have lengths of 30 cm and 40 cm. What is the height of the triangle? - Calculate 66254
 Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm.
Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm.
- Flowing 66174
 How long in an hour will a 30m, 15m, and 2m pool be filled with water flowing at 900l / min if it is 90% full?
How long in an hour will a 30m, 15m, and 2m pool be filled with water flowing at 900l / min if it is 90% full? - Circumference 66134
 The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid.
The isosceles trapezoid ABCD has an area of 36 cm². One of its bases is two times longer than the other. Height is 4 cm. Calculate the circumference of the trapezoid. - Cylindrical 66114
 The cylindrical vase has a volume of 1 l. Calculate the height of the vase if its base has an area of 0.5 dm².
The cylindrical vase has a volume of 1 l. Calculate the height of the vase if its base has an area of 0.5 dm². - Interest 66024
 How much do I have to save per month to save CZK 100,000 in 5 years if the interest rate is 4%, the interest period is one month, and the interest tax is 15%?
How much do I have to save per month to save CZK 100,000 in 5 years if the interest rate is 4%, the interest period is one month, and the interest tax is 15%? - Vertically 65984
 We threw the stone vertically upwards at a speed of v = 15m. s-1. How long will it be at a) 10 m, b) 12 m?
We threw the stone vertically upwards at a speed of v = 15m. s-1. How long will it be at a) 10 m, b) 12 m?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
Tip: Our volume units converter will help you convert volume units. See also more information on Wikipedia.
