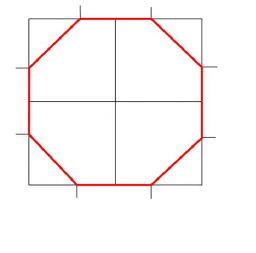
Octagon perimeter area
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm2.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Board triangle ratio
 From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area.
From a rectangular board with 2 m and 3 m dimensions, we cut isosceles and right-angled triangles at the corners with an overhang of 40 cm. Calculate the ratio of the rest of the board's areas to its total original area. - Octagon from rectangle
 We cut the corners of a rectangular tablecloth with dimensions of 4 dm and 8 dm into isosceles triangles. Thus, the octagon formed had an area of 26 dm². How many dm² of tablecloth do we cut down?
We cut the corners of a rectangular tablecloth with dimensions of 4 dm and 8 dm into isosceles triangles. Thus, the octagon formed had an area of 26 dm². How many dm² of tablecloth do we cut down? - Triangle calculations
 a) The perimeter of the equilateral triangle ABC is 63 cm. Calculate the side sizes of the triangle and its height. b) A right isosceles triangle has an area of 40.5 square meters. How big is his circuit? c) Calculate the square's area if the diagonal's s
a) The perimeter of the equilateral triangle ABC is 63 cm. Calculate the side sizes of the triangle and its height. b) A right isosceles triangle has an area of 40.5 square meters. How big is his circuit? c) Calculate the square's area if the diagonal's s - Recursion squares
 In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 20 cm. Calculate: a) the sum of peri - Octagon
 We have a square with a side 56 cm. We cut corners to make his octagon. What will be the side of the octagon?
We have a square with a side 56 cm. We cut corners to make his octagon. What will be the side of the octagon? - Resulting cross
 From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross?
From the corners of the square with a side length of 10 cm, we cut out small squares with a side length of 3 cm. What is the area of the resulting cross? - Isosceles Triangle Interior Angles
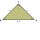 The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles.
The area of the isosceles triangle is 8 cm2, and its arm's length is 4 cm. Calculate the sizes of its interior angles.
